第一次周报

发表于 更新于 分类于

内容：

  1. mlapp进度：第一章、第二章的65%
  2. BPR: Bayesian Personalized Ranking from Implicit Feedback (精读)
  3. Jure leskovec cs224w 课程进度50%

1 简介

1.1 是什么以及为什么

数据的泛滥要求有对数据进行自动分析的方法，这便是机器学习所能解决的问题。我们定义机器学习（Machine Learning）为一系列可以自动挖掘数据中潜在模式的方法，并且利用发现的模式去预测未来的数据，或者在不确定的情况下执行其他的决策

在很多领域中，数据都呈现出一种长尾（long tail）效应，意味着经常发生的那些事件往往是很少的，大部分事件是很少发生的。比如说，我们经常遇到的那些单词往往也就是那么一小部分（比如“the”和“and”），但是大部分单词（比如“pareidolia”）却很少使用。类似的，有些电影和书很有名，但大部分并非如此。章节2.4.7将进一步介绍长尾效应。长尾效应所导致的一个结果是：我们只需要较少的数据就可以预测或者理解大部分行为。

分类：监督方法——分类和回归任务

​ 无监督方法：模型的目标是在数据中找到“感兴趣的模式”。有时也称这种方法为知识发掘（knowledge discovery）

​ 强化学习：在随机的奖励或者惩罚信号的情况下，模型可以更好地学习采取什么的行为。

1.2 监督学习（Supervised learning）

1.2.1 分类

  1. 二分类

  2. 多分类

  3. 多标签分类：类别的标签彼此之间互不排斥（比如某人可以被归类为高的和强壮的），更好的方式是将它理解为预测多个相关二元类标签的问题（即所谓的多变量输出模型)

    MAP： \[ \hat{y}=\hat{f}(\mathbf{x})=\arg \max_{c=1}^C\ p(y=c|\mathbf{x},\mathcal{D}) \tag{1.1} \] 当P远小于1的情况下，这种情况下，我们对这个选择并不是很确定，所以相较于给出这个不信任的答案，直接指出“我不知道”可能会更好，这在医疗或者金融等需要规避风险的领域尤其重要。

1.2.1 回归

回归所输出的变量是连续的。

在现实世界中的一些回归问题。

  • 基于当前市场的情况和一些其他的辅助信息预测明天的股票价格；

  • 预测一个观看YouTube上特定视频的观众的年龄；

  • 给定机器人各电机的控制信号(扭矩)，预测机器人手臂末端执行器在三维空间中的位置；

  • 根据多种不同临床测量数据预测前列腺特异性抗原(PSA)在体内的数量；

  • 使用天气数据，时间等信息预测某建筑内任意位置的温度。

1.3无监督学习

  1. 非监督学习是一个无条件概率估计

  2. 往往需要针对特征向量建立一个多变量概率模型

1.3.1 发现聚类

  1. 在监督学习中，我们会被告知预测值有多少个类别，但在非监督学习中，我们可以自由选择簇（类）的数目。P(K|D)
  2. 估计每个数据点属于哪一个簇——P(zi=k|xi, D)

1.3.2 发现潜在因子(Discovering latent factors)

降维背后的动力在于尽管实际的数据可能是高维的，但其可能只有少量的主导因素，这些潜在的主导因素被称为潜在因子（latent factors）。

1.3.3 发现图结构(Discovering graph structure)

其中图节点表示变量，边表示变量之间的直接依赖关系。稀疏图的学习主要有两种应用:发现新知识和获得更好的联合概率密度估计器。

1.3.4矩阵补全(Matrix completion)

  1. 图像修复(Image inpainting)

  2. 协同过滤(Collaborative filtering)——共现矩阵的补全

  3. 购物篮分析(Market basket analysis)——频繁项集挖掘（frequent itemset mining）

    基于概率的方法不好解释

    这是数据挖掘和机器学习的典型区别:在数据挖掘中，更强调可解释模型，而在机器学习中，更强调准确的模型。

1.4 机器学习中的一些基本概念

#### 1.4.1参数模型和非参数模型（参数量的区别）

模型是否具备固定的参数数量，或者说参数数量是否随训练样本的增加而增加。前者被称为参数模型（parametric model），后者被称为非参数模型（non-parametric model）。

  1. 非参数分类器：K近邻（K-nearest neighbors）

    参考距离该点最近的K个训练集中的样本（投票选出class）

\[ xp(y=c|\mathbf{x},\mathcal{D},K)=\frac{1}{K}\sum_{i\in N_K(\mathbf{x},\mathcal{D})}\mathbb{I}(y_i=c) \tag{1.2} \]

\[  \mathbb{I}(e)=\begin{cases}1, & \mbox{if }e\mbox{ is true} \\0, & \mbox{if }e\mbox{ is false}\end{cases} \tag{1.3} \]

被称为基于存储的学习（memory-based learning）或者基于样例的学习（instance-based learning）。在这个方法中，最常用的距离测度为欧氏距离（该距离将这个技术限制在了实数领域），尽管其他的测度也可以使用。当K=1时，KNN分类器将得到关于所有点的泰森多边形图.

推荐系统中item-KNN 用到了基于社交的相似度计算法 。计算A与B的相似度，则是找到所有买过A的又买过B的用户，考虑评价偏差，计算完成后我们得到k个最相似的item。

维度灾难（curse of dimensionality）

KNN分类器十分简单且效果很好，其前提是需要一个好的距离测度以及足够多的标记数据。然而，KNN的劣势在于它不适用于高维输入。造成这个问题的原因是维度灾难（curse of dimensionality）。当维度上升是，数据分布会相对稀疏，丧失“局部性”

1.4.2 分类和回归中的参数模型

  1. 线性回归

\[ y(\mathbf{x})=\mathbf{w}^T\mathbf{x}+\epsilon =\sum_{j=1}^Dw_jx_j+\epsilon \tag{1.4} \]

epsilon 服从高斯分布$ N(mu, sigma^2)$ , 重写为： \[ p(y|\mathbf{x},\mathbf{\theta})=\mathcal{N}(y|\mu(\mathbf{x}),\sigma^2(\mathbf{x})) \tag{1.5} \] 噪声固定的情况下： \[ x\mu(\mathbf{x})=w_0+w_1x=\mathbf{w}^T\mathbf{x} \tag{1.6} \] 线性回归模型同样可以对非线性关系进行建模（基函数拓展）： \[ p(y|\mathbf{x},\mathbf{\theta})=\mathcal{N}(y|\mathbf{w}^T\phi(\mathbf{x}),\sigma^2) \tag{1.7} \]

  1. 逻辑回归

将y分布转换为伯努利分布： \[ p(y|\mathbf{x},\mathbf{w})={\rm{Ber}}(y|\mu(\mathbf{x}))\tag{1.8} \]

\[ \mu(x) = {\rm{sigm}}(\eta) \] \[ {\rm{sigm}}(\eta)\triangleq\frac{1}{1+\exp(-\eta)}=\frac{e^\eta}{e^\eta+1} \tag{1.10} \] 术语"sigmoid"表示S型：如图1.19(a)所示。它又被称为压缩函数，因为它将整个实轴映射到了区间[0,1] \[ p(y|\mathbf{x},\mathbf{w})={\rm{Ber}}(y|{\rm{sigm}}(\mathbf{w}^T\mathbf{x})) \tag{1.11} \]

1.4.3 过拟合(Overfitting)

应该避免对输入中的任何微小的变化进行建模，因为那些微小的变化很有可能是噪音而非真实的信号。

1.4.4 模型选择

1.4.5 没有免费的午餐理论(No free lunch theorem)

All models are wrong, but some models are useful.—George Box

对于每个模型，可能有很多不同算法去训练它们，且不同算法都在速度—精度—复杂度之间权衡

2 概率

概率的两种解释：

  1. 频率派：概率代表事件在长时间实验的情况下出现的频率。

  2. 贝叶斯派：概率是用来量化我们对于某些事件的不确定度（uncertainty） 贝叶斯解释的一个重要优势在于，它可以用来衡量那些无法进行重复试验的事件的不确定度。

2.2.2 基本定理

  1. 并集发生概率 \[ \begin{align}p(A\or B) &= p(A)+p(B)-p(A\or B) \tag{2.1} \\&=p(A)+p(B) \ 如果A和B互斥 \tag{2.2} \\\end{align} \]

  2. 联合概率 \[ p(A,B)=p(A\and B)=p(A|B)p(B) \tag{2.3} \] 边缘概率（离散求和，连续积分）： （求和法则（sum rule）或者叫全概率法则（rule of total probability） \[ p(A)=\sum_b p(A,B)=\sum_b p(A|B=b)p(B=b) \tag{2.4} \] 链式法则（chain rule） \[ p(X_{1:D})=p(X_1)p(X_2|X_1)p(X_3|X_2,X_1)...p(X_D|X_{1:D-1}) \tag{2.5} \] 1:D代表集合{1,2,3,...D}

  3. 条件概率

\[ p(A|B)=\frac{p(A,B)}{p(B)} \ {\rm{if}} \ p(B)\gt 0 \tag{2.6} \] 4. 贝叶斯定理 \[ p(X=x|Y=y)=\frac{p(X=x,Y=y)}{p(Y=y)}=\frac{p(X=x)p(Y=y|X=x)}{\sum_{x^\prime}p(X=x^\prime)p(Y=y|X=x^\prime)} \tag{2.7} \]

2.2.3 生成式分类器

\[ p(y=c|\mathbf{x})=\frac{p(y=c)p(\mathbf{x}|y=c)}{\sum_{c^\prime}p(y=c^\prime|\mathbf{\theta})p(\mathbf{x}|y=c^\prime)} \tag{2.13} \]

生成式分类器(generative classifier)，因为它通过使用类条件概率密度\(p(\mathbf{x}|y=c)\)和类先验分布\(p(y=c)\)来指定如何生成样本。

2.2.4 独立性和条件独立性

  1. 独立：

    如果两个随机变量x和Y的联合概率分布可以表示为边缘分布的乘积，则称X和Y是无条件独立(unconditionally independent)或者边缘独立(marginally independent)的

  2. 条件独立：联合分布等于条件边缘分布的乘积,已知z情况下：x,y是独立的 \[ p(X,Y|Z)=p(X|Z)p(Y|Z) \tag{2.15} \] X Y| Z 则意味着存在着函数 g 和 h ，对全部的x,y,z，在p(z)>0的情况下满足下列关系： \[ p(x,y|z) = g(x,z)h(y,z) \tag{2.16} \] 条件独立性假设允许我们通过一些局部信息去构建大规模的概率模型。

2.2.5 连续随机变量

X是个连续随机变量，有： \[ \begin{aligned}A & =(X\le a)\\B & =(X\le B)\\W & =(a\le X\le b)\end{aligned} \] 有: \[ B=A\bigvee W \] \[ p(B)=p(A)+p(W) \] \[ p(w)=p(B)-p(A) \] X 的连续分布函数（cumulative distribution function，缩写为 cdf）: \[ F(q) \overset\triangle{=} p(X\le q) \] 这个 cdf 是一个单调递增函数（monotonically increasing function）

2.2.6 分位数

cdf反函数，F^{-1}(0.5)为分布中位数：一半的概率质量分布在左边，另一半分布在右边。

2.2.7 期望和方差

\[ \mathrm{E}[X] \overset\triangle{=} \sum_{x\in X}x p(x) \]

\[ \begin{aligned}var[X] & =E[(X-\mu)^2]=\int(x-\mu)^2p(x)dx &\text{ (2.24)}\\& = \int x^2p(x)dx +\mu^2 \int p(x)dx-2\mu\int xp(x)dx=E[X^2]-\mu^2 & \text{ (2.25)}\\\end{aligned} \]

\[ E[X^2]= \mu^2+\sigma^2 \]

\[ std[X]\overset\triangle{=} \sqrt {var[X]} \]

2.3 常见的离散分布

  1. 二项分布

    pmf: \[ {X\sim Bin(n,\theta)} Bin(k|n,\theta)\overset\triangle{=} \binom{n}{k} \theta ^k (1- \theta)^{n-k} \] 均值方差： \[ mean=\theta, var =n\theta(1-\theta) \]

  2. 伯努利分布

    伯努利分布只是二项分布中 n=1 的特例 \[ Ber(x|\theta)=\begin{cases} \theta &\text{ if x =1} \\ 1-\theta &\text{ if x =0} \end{cases} \]

  3. 多项式分布:对有 K 个可能结果的事件进行建模，就要用到多项分布（multinomial distribution） \[ Mu(x|n,\theta) = \binom {n}{x_1,..,x_K}\prod^K_{j=1}\theta^{x_j}_j \]

  4. 多重伯努利分布

  5. 泊松分布

  6. ...

BPR: Bayesian Personalized Ranking from Implicit Feedback

Uncertainty in Artificial Intelligence (UAI) 2009 ——目前CCF B

作者： Steffen Rendle （google 推荐大佬）

背景

  1. senario： implicit feedback

  2. 当时的item-recommendation方法没有针对排序（ranking）进行排序

BPR本身并不优化用户对物品的评分，而只借由评分来优化用户对物品的排序 即：it is a real ranking algorithm.

贡献

  1. 后验概率推出BPR优化目标； 探讨和AUC的关系
  2. 优化算法learnBPR - SGD
  3. 展示如何应用到item-Knn以及MF；对比了WR-MF、MMMF
  4. 实验证明比其他方法好（包括比non-personalized 理论值）

算法速成

1数据pair化预处理：

BPR算法将用户对物品的评分（显示反馈“1”，隐式反馈“0”）处理为一个pair对的集合<i,j>，其中i为评分为1的物品，j为评分为0的物品。假设某用户有M个“1”的评分，N个“0”的评分，则该用户共有M*N个pair对。这样数据集就由三元组 <u,i,j>表示，该三元组的物理含义为：相对于物品“j”，用户“u”更喜欢物品“i”。

2假设

  1. 一是每个用户之间的偏好行为相互独立，即用户u在商品i和j之间的偏好和其他用户无关

  2. 是同一用户对不同物品的偏序相互独立，也就是用户u在商品i和j之间的偏好和其他的商品无关。

  3. P(θ) 服从高斯分布（？）

问题：假设是否合理？

我觉得现在来看前两个假设太强了

3 BPR优化目标推导*

排序关系符号$ >u $:

完整性：\(∀i,j∈I:i≠j⇒i>uj∪j>ui ∀i,j∈I:i≠j⇒i>uj∪j>ui\) (i,j 不等，i >u j 或j>u i至少有一个)

反对称性：\(∀i,j∈I:i>uj∩j>ui⇒i=j ∀i,j∈I:i>uj∩j>ui⇒i=j\) （如果既有i>u j 又有 j>ui, 说明i,j是同一个）

传递性：\(∀i,j,k∈I:i>u j∩j>uk⇒i>uk\)

BPR 基于最大后验估计P(W,H|>u)来求解模型参数W,H,用θ来表示参数,>u代表用户u对应的所有商品的全序关系,则优化目标是P(θ|>u)。根据贝叶斯公式，我们有： \[ P(\theta|>_u) = \frac{P(>_u|\theta)P(\theta)}{P(>_u)} \]

\[ P(\theta|>_u) \propto P(>_u|\theta)P(\theta) \]

  • 第一部分：优化目标转化为两部分。第一部分和样本数据集D有关，第二部分和样本数据集D无关。 \[ \prod_{u \in U}P(>_u|\theta) = \prod_{(u,i,j) \in (U \times I \times I)}P(i >_u j|\theta)^{\delta((u,i,j) \in D)}(1-P(i >_u j|\theta))^{\delta((u,j,i) \not\in D) } \]

    \[ \delta(b)= \begin{cases} 1& {if\; b\; is \;true}\\ 0& {else} \end{cases} \]

根据完整性和反对称性，优化目标的第一部分可以简化为： \[ \prod_{u \in U}P(>_u|\theta) = \prod_{(u,i,j) \in D}P(i >_u j|\theta) \]

尝试用\(sigmoid\)表示\(P(i>uj|θ)\)这个概率: \[ P(i >_u j|\theta) = \sigma(\overline{x}_{uij}(\theta)) \]

\[ \begin{align*} \sigma(x)&=\frac{1}{1+e^{-x}} \end{align*} \]

  • 第二部分：作者大胆使用了贝叶斯假设，即这个概率分布符合正太分布，且对应的均值是0，协方差矩阵是\(\lambda_{\theta}I\)

\[ P(\theta) \sim N(0, \lambda_{\theta}I) \]

高斯分布： [公式]

[公式]

为什么使用0均值正态分布假设？

1.简化计算？ \(lnP(\theta) = \lambda||\theta||^2\)

2.引出正则项？

前两项结合，优化目标推导：

image-20211021194242238

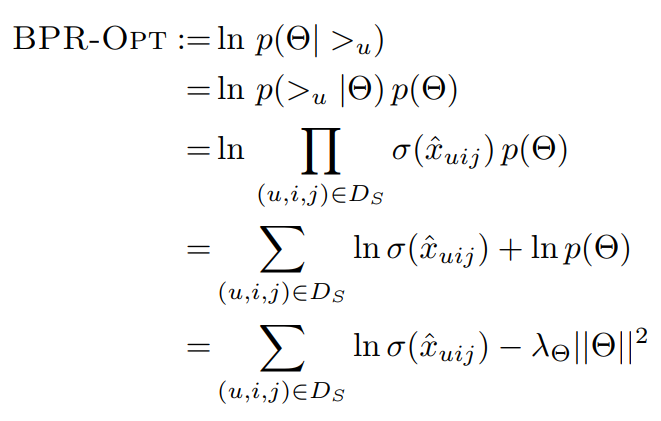
对参数求导：

image-20211021200205448

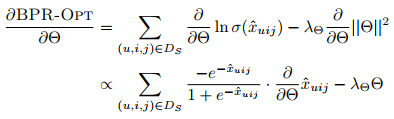
注：f′(x)=f(x)∗(1−f(x)) \[ \begin{align*} sigmoid^{'}(x)&=(\frac{1}{1+e^{-x}})^{'} \\ &=\frac{1}{1+e^{-x}}e^{-x}(-1)\\ &=\frac{e^{-x}}{(1+e^{-x})^2}\\ &=\frac{1}{1+e^{-x}}(1-\frac{1}{1+e^{-x}})\\ &=sigmoid(x)(1-sigmoid(x)) \end{align*} \]

使用SGD进行优化 image-20211021200345228

4 亿些细节

  1. 与AUC的关系

    AUC：

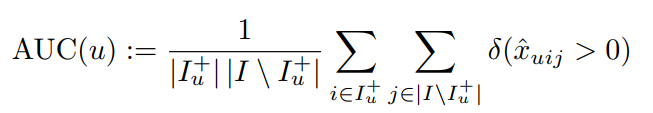
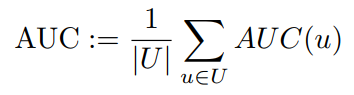
    image-20211021230825086

    使用论文notation：

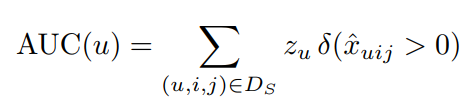
    image-20211021230915429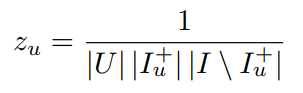
    image-20211021231013168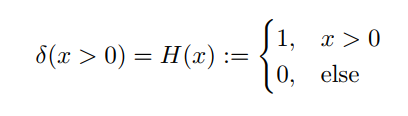
    image-20211021232005411

  2. 应用于knn和MF

    MF：

    用了和funkSVD类似的矩阵分解模型，这里BPR对于用户集U和物品集I的对应的\(U×I\)的预测排序矩阵\(\overline{X}，\)我们期望得到两个分解后的用户矩阵\(W(|U|×k)\)和物品矩阵\(H(|I|×k)\)，满足 \[ \overline{X}=WHT \]

    \[ \overline{x}_{ui} = w_u \bullet h_i = \sum\limits_{f=1}^kw_{uf}h_{if} \]

    \[ \frac{\partial (\overline{x}_{ui})}{\partial \theta} = \begin{cases} (h_{if}-h_{jf})& {if\; \theta = w_{uf}}\\ w_{uf}& {if\;\theta = h_{if}} \\ -w_{uf}& {if\;\theta = h_{jf}}\end{cases} \]

    itemKNN：

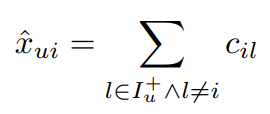
    image-20211022182610996

    相似度矩阵C : I × I

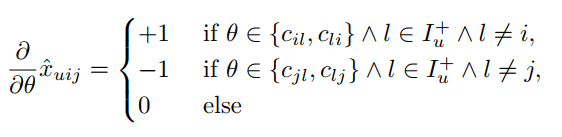
    image-20211021232313915

  3. 实验结果

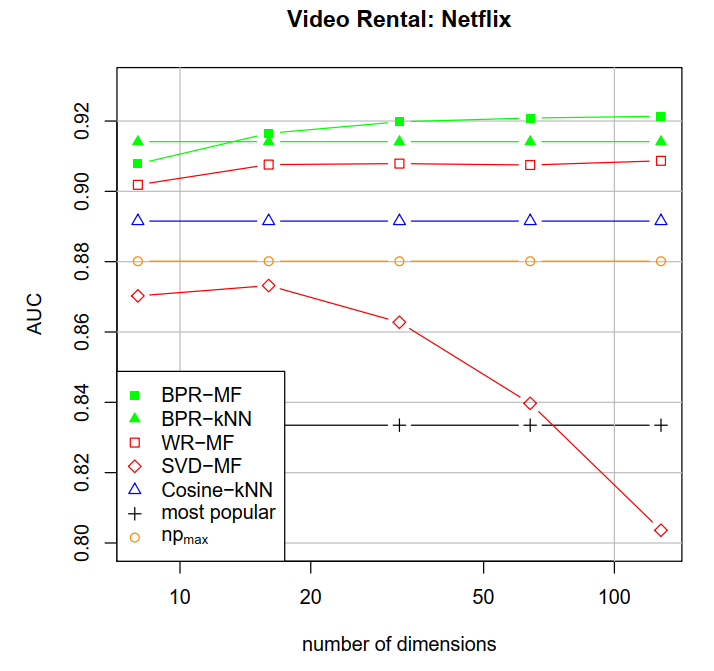
    使用了Rossann和Netflix数据集进行实验。使用AUC测评：

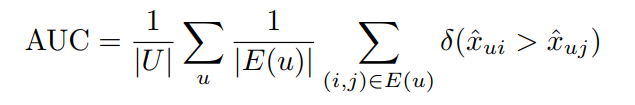
    image-20211021225104841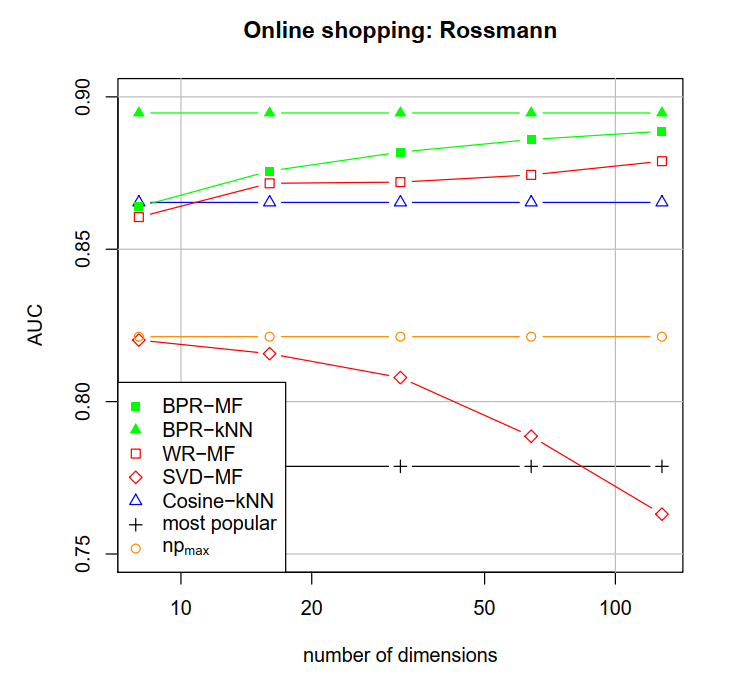
    image-20211021204544627
image-20211021205021673

问题：bootstrap应该会有没采到的吧？会有影响吗？

BPRLoss

BPR Loss 的思想很简单，就是让正样本和负样本的得分之差尽可能达到最大.

BPRLoss