第二次周报

发表于 更新于 分类于

week 2 内容：

  • Jure leskovec cs224w 课程进度80%（作业进度60%）

  • 论文阅读：FM、NGCF、light-gcn、cluster-GCN

  • 毕设准备

GNN

GCN

就像"卷积"这个名字所指代的那样，这个想法来自于图像，之后引进到图（Graphs）中。然而，图像有固定的结构时，而图（Graphs）就复杂得多，结构不定。

img

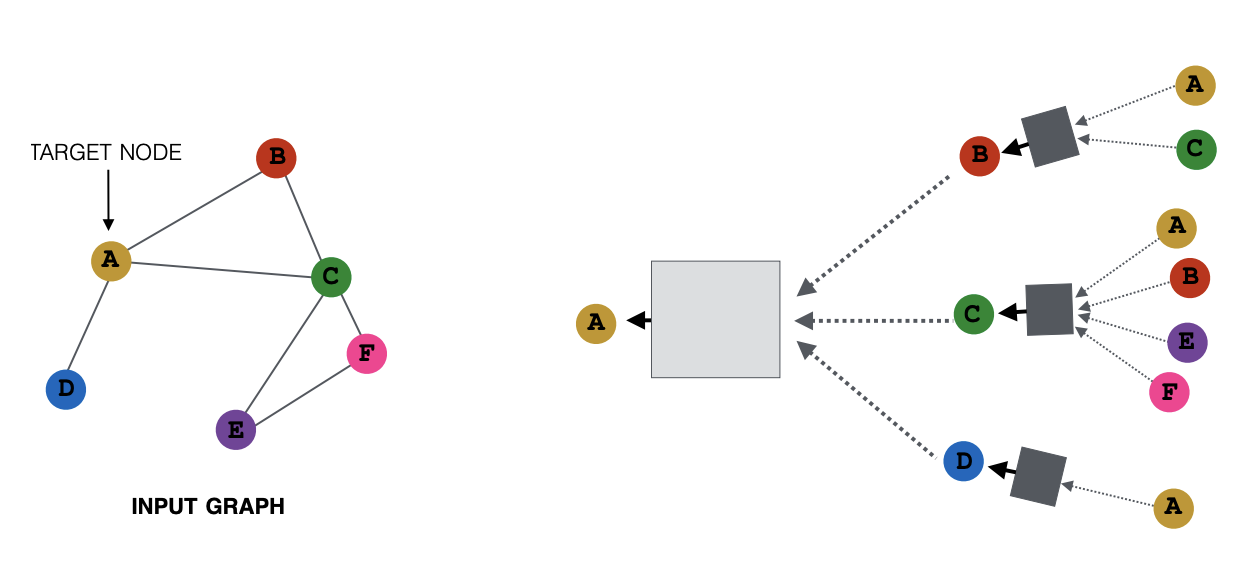
computation_graph_for_a

两个步骤：

  1. propagation（message passing)

  2. aggregation

\[ h_v^{(l)} = W_l\cdot h_v^{(l-1)} + W_r \cdot AGG(\{h_u^{(l-1)}, \forall u \in N(v) \}) \]

\[ AGG(\{h_u^{(l-1)}, \forall u \in N(v) \}) = \frac{1}{|N(v)|} \sum_{u\in N(v)} h_u^{(l-1)} \]

在这里插入图片描述
GQNyxe.png

GraphSage

  • 在 aggregate 的形式上做了进一步扩展—GraphSAGE的想法是采用一个通用的aggregation函数来表示黑箱的运算，可以采用不同的方法聚合其邻居，然后再将其与自身特征拼接

  • 除了 mean，其实任意的将多个 embedding 映射到一个 embedding 的函数都可以用来做聚合，例如 pool，例如 LSTM，

    在这里插入图片描述

cluster-GCN

https://blog.csdn.net/sinat_26811377/article/details/97810302

聚类总结

metis

目前基于SGD的gcn算法，大规模GCN的训练面临问题：

1）面临随着gcn层数增长，计算复杂度呈指数增长；

2）需要保存整个Graph和每个node的embedding，存储量巨大。

Cluster-GCN通过graph聚类算法来筛选联系紧密的sub-graph，从而在sub-graph中的一组node进行采样，并且限制该sub-graph中的邻居搜索，可以显著提高搜索效率。

在这里插入图片描述
  1. metis和graclus谱聚类
  2. for循环，每次随机选一个cluster（without replacement，不放回）计算subgraph的梯度进行更新
  3. 直至优化完成

GNN在推荐(协同过滤)领域应用

Neural Collaborative Filtering

CF发展

NCF不如MF？

img

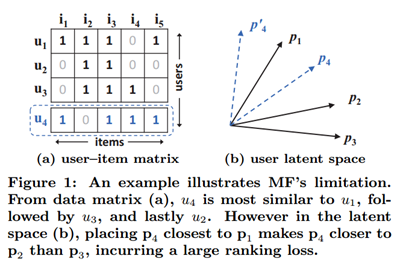
研究点：

  • 关于推荐系统的深度学习研究不多；

  • 对user和item的交互行为（interaction）的建模大多使用MF，对user和item的隐特征使用内积计算，而这是一种线性方式。而通过引入user/item偏置，提高MF效果也说明内积不足以捕捉到用户交互数据中的复杂结构信息。

模型框架：

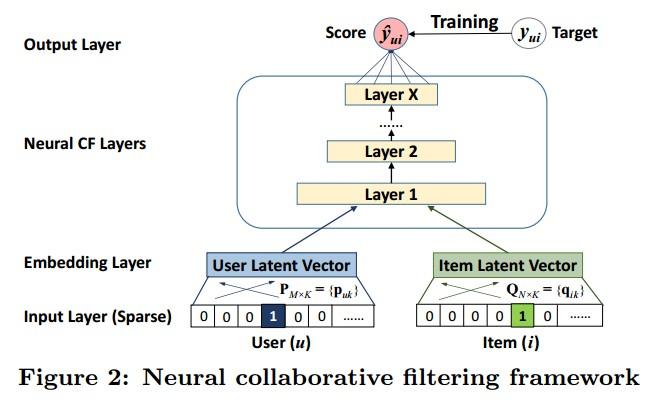
【导读】Neural Collaborative Filtering

这里关注的问题：

并没有把user和item的交互信息本身编码进 embedding 中，而NGCF希望显式建模User-Item 之间的高阶连接性来提升 embedding。

图神经网络应用

NGCF（SIGIR 2019）

在这里插入图片描述

推荐领域的user-item交互可以被看做是一个二部图。

High-order Connectivity 解释高阶连通性如上图，图1左边为一般CF中user-item交互的二部图，双圆圈表示此时需要预测的用户u1，对于u1我们可以把有关他的连接扩展成右图的树形结构，l是能到达的路径长度（或者可以叫跳数），l=1表明能一步到达u1的item，此时可以看到最外层的跳数相同的i4跟i5相比（l都为3），用户u1对i4的兴趣可能要比i5高，因为i4->u2->i2->u1、i4->u3->i3->u1有两条路径，而i5->u2->i2->u1只有一条，所以i4的相似性会更高。所以如果能扩展成这样的路径连通性来解释用户的兴趣，就是高阶连通性。

完整模型：

在这里插入图片描述

NGCF的完整模型如下图，可以分为三个部分来看：

Embeddings：对user和item的嵌入向量，普通的用id来嵌入就可以了 Embedding Propagation Layers：挖掘高阶连通性关系来捕捉交互以细化Embedding的多个嵌入传播层 Prediction Layer：用更新之后带有交互信息的 user 和 item Embedding来进行预测

message passing：

$ m_{u i}=(W_{1} e_{i}+W_{2}(e_{i} e_{u})) $

使用embedding后的user，item的特征$ e_u $ 、\(e_i\) 作为输入，然后两者计算内积相似度来控制邻域的信息，再加回到item上，用权重W控制权重，最后的N是u和i的度用来归一化系数，可以看做是折扣系数，随着传播路径长度的增大，信息慢慢衰减。

aggregation：

\(e_{u}^{(1)}=\operatorname{LeakyReLU}\left(m_{u \leftarrow u}+\sum_{i \in N_{u}} m_{u \leftarrow i}\right)\)

3-hop计算图：

在这里插入图片描述

\(E^{(l)}=\sigma\left((L+I) E^{(l-1)} W_{1}^{(l)}+L E^{(l-1)} \odot E^{(l-1)} W_{2}^{(l)}\right)\)

light-GCN(SIGIR 2020)

在这里插入图片描述

NGCF主要遵循标准GCN变形得到，包括使用非线性激活函数和特征变换矩阵w1和W2。然而作者认为实际上这两种操作对于CF并没什么0用，理由在于不管是user还是item，他们的输入都只是ID嵌入得到的，即根本没有具体的语义（一般在GCN的应用场景中每个节点会带有很多的其他属性），所以在这种情况下，执行多个非线性转换不会有助于学习更好的特性；更糟糕的是，它可能会增加训练的困难，降低推荐的结果。

\(\begin{aligned} e_{u}^{(k+1)} &=\sum_{i \in N_{u}} \frac{1}{\sqrt{\left|N_{u}\right|} \sqrt{\left|N_{i}\right|}} e_{i}^{(k)} \\ e_{i}^{(k+1)} &=\sum_{u \in N_{i}} \frac{1}{\sqrt{\left|N_{i}\right|} \sqrt{\left|N_{u}\right|}} e_{u}^{(k)} \end{aligned}\)

只聚合连接的邻居，连自连接都没有。最后的K层就直接组合在每个层上获得的嵌入，以形成用户（项）的最终表示:

\(\begin{array}{c} e_{u}=\sum_{k=0}^{K} \alpha_{k} e_{u}^{(k)} \\ e_{i}=\sum_{k=0}^{K} \alpha_{k} e_{i}^{(k)} \end{array}\)

其中\[ α_k=1 / (k+1) \]

为什么要组合所有层？

  • GCN随着层数的增加会过平滑，直接用最后一层不合理
  • 不同层的嵌入捕获不同的语义，而且更高层能捕获更高阶的信息，结合起来更加全面
  • 将不同层的嵌入与加权和结合起来，可以捕获具有自连接的图卷积的效果，这是GCNs中的一个重要技巧