第八次周报

发表于 2022-01-24 更新于 2022-06-28 分类于周报

week 8 内容：

louis philippe morency 《多模态机器学习》 70%
论文阅读：
1. Variational Autoencoders for Collaborative Filtering
2. A Survey on Curriculum Learning（TPAMI 2021）
3. sampling
4. VI、EM算法、GMM

Variational Autoencoders for Collaborative Filtering（WWW 2018）

主要工作

该文作者把变分自编码器拓展应用于基于隐式反馈的协同过滤推荐任务，希望通过非线性概率模型克服线性因子模型的局限。该文提出了基于变分自编码器（Variational Autoencoder）的生成模型VAE_CF，并针对变分自编码器的正则参数和概率模型选取做了适当调整（使用了多项式分布），使其在当时推荐任务中取得SOTA结果。

模型

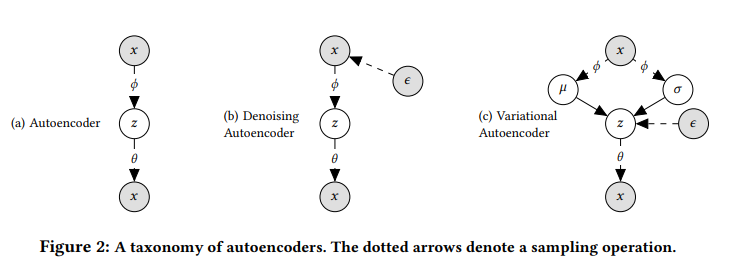
如上图所示，虚线代表了采样操作，a是传统AE，b是denoising AE（论文中使用了多项式分布的Mult-dae）， c代表vae（论文中是mult-vae）。

$\mathbf{z}_u \sim \mathcal{N}(0, \mathbf{I}_K), \pi(\mathbf{z}_u) \propto \exp\{f_\theta (\mathbf{z}_u\},\mathbf{x}_u \sim \mathrm{Mult}(N_u, \pi(\mathbf{z}_u))$

该模型根据标准高斯分布抽取K维隐变量 $z_{u} \sim \mathcal{N}(0,I_{K})$ ，然后根据非线性函数 $f_{\theta}(\cdot)$ 生成用户 $u$ 点击所有物品的概率分布 $\pi（z_{u}）\propto exp(f_{\theta}(z_{u}))$ ，最后根据多项式分布 $x_{u} \sim Mult(N_{u},\pi(z_{u}))$ 重构用户点击历史（隐式反馈的用户-物品评价矩阵对应行)。

Multi-DAE目标函数(对数似然)：

$\mathcal{L}_u(\theta, \phi) = \log p_\theta(\mathbf{x}_u | g_\phi(\mathbf{x}_u))$

Multi-VAE目标函数（ELBO）：

$\mathcal{L}_u(\theta, \phi) = \mathbb{E}_{q_\phi(z_u | x_u)}[\log p_\theta(x_u | z_u)] - \beta \cdot KL(q_\phi(z_u | x_u) \| p(z_u))$

VAE_CF模型较标准的变分自编码器做了如下调整：

1、将正则参数调至0.2（低于常规值1，具体来说使用了annealing来逐步增大beta），称其为部分正则化（partially regularized)，实际上是$-vae $在推荐上的应用。

2、使用了多项式分布进行重建而非高斯分布。

多项式似然非常适合于隐式反馈数据的建模，并且更接近 rank loss；
无论数据的稀缺性如何，采用principled Bayesian方法都更加稳健。

使用SGD进行优化：

代码

class MultiVAE(nn.Module):
    """
    Container module for Multi-VAE.

    Multi-VAE : Variational Autoencoder with Multinomial Likelihood
    See Variational Autoencoders for Collaborative Filtering
    https://arxiv.org/abs/1802.05814
    """

    def __init__(self, p_dims, q_dims=None, dropout=0.5):
    	# p_dims = [200, 600, n_items]
        super(MultiVAE, self).__init__()
        # q -> encoder | p-> decoder
        self.p_dims = p_dims
        # 确定维度
        if q_dims:
            assert q_dims[0] == p_dims[-1], "In and Out dimensions must equal to each other"
            assert q_dims[-1] == p_dims[0], "Latent dimension for p- and q- network mismatches."
            self.q_dims = q_dims
        else:
            self.q_dims = p_dims[::-1] # [n_items, 600, 200]

        # Last dimension of q- network is for mean and variance
        temp_q_dims = self.q_dims[:-1] + [self.q_dims[-1] * 2] # [ n_items, 600, 400] ]
        # encoder
        # in:[ n_items, 600]
        # out:[600, 400]
        self.q_layers = nn.ModuleList([nn.Linear(d_in, d_out) for
            d_in, d_out in zip(temp_q_dims[:-1], temp_q_dims[1:])])
        # decoder
        # in:[200, 600,]
        # out:[600, n_items]
        self.p_layers = nn.ModuleList([nn.Linear(d_in, d_out) for
            d_in, d_out in zip(self.p_dims[:-1], self.p_dims[1:])])
        
        self.drop = nn.Dropout(dropout)
        self.init_weights()
    
    def forward(self, input):
        mu, logvar = self.encode(input)
        z = self.reparameterize(mu, logvar)
        return self.decode(z), mu, logvar
    
    def encode(self, input):
        h = F.normalize(input)
        h = self.drop(h)
        
        for i, layer in enumerate(self.q_layers):
            h = layer(h)
            if i != len(self.q_layers) - 1:
                h = F.tanh(h)
            else:
                # 最后一层分均值和方差
                mu = h[:, :self.q_dims[-1]]
                logvar = h[:, self.q_dims[-1]:]
        return mu, logvar

    def reparameterize(self, mu, logvar):
        # 重参数化技巧
        if self.training:
            std = torch.exp(0.5 * logvar)
            eps = torch.randn_like(std)
            return eps.mul(std).add_(mu)
        else:
            return mu
    
    def decode(self, z):
        # 解码
        h = z
        for i, layer in enumerate(self.p_layers):
            h = layer(h)
            if i != len(self.p_layers) - 1:
                h = F.tanh(h)
        return h

    def init_weights(self):
        for layer in self.q_layers:
            # Xavier Initialization for weights
            size = layer.weight.size()
            fan_out = size[0]
            fan_in = size[1]
            std = np.sqrt(2.0/(fan_in + fan_out))
            layer.weight.data.normal_(0.0, std)

            # Normal Initialization for Biases
            layer.bias.data.normal_(0.0, 0.001)
        
        for layer in self.p_layers:
            # Xavier Initialization for weights
            size = layer.weight.size()
            fan_out = size[0]
            fan_in = size[1]
            std = np.sqrt(2.0/(fan_in + fan_out))
            layer.weight.data.normal_(0.0, std)

            # Normal Initialization for Biases
            layer.bias.data.normal_(0.0, 0.001)

def loss_function(recon_x, x, mu, logvar, anneal=1.0):
    # BCE = F.binary_cross_entropy(recon_x, x)
    BCE = -torch.mean(torch.sum(F.log_softmax(recon_x, 1) * x, -1))
    KLD = -0.5 * torch.mean(torch.sum(1 + logvar - mu.pow(2) - logvar.exp(), dim=1))

    return BCE + anneal * KLD

A Survey on Curriculum Learning （TPAMI 2021）

主要工作

课程学习 (Curriculum learning, CL) 是近几年逐渐热门的一个前沿方向。Bengio 首先提出了课程学习（Curriculum learning，CL）的概念，它是一种训练策略，模仿人类的学习过程，主张让模型先从容易的样本开始学习，并逐渐进阶到复杂的样本和知识（从易到难）。CL策略在计算机视觉和自然语言处理等多种场景下，在提高各种模型的泛化能力和收敛率方面表现出了强大的能力。这篇综述一共调研了147篇文献，从问题定义、有效性分析、方法总结、未来研究方向等几大方面进行了详细的概括和总结。

问题定义：

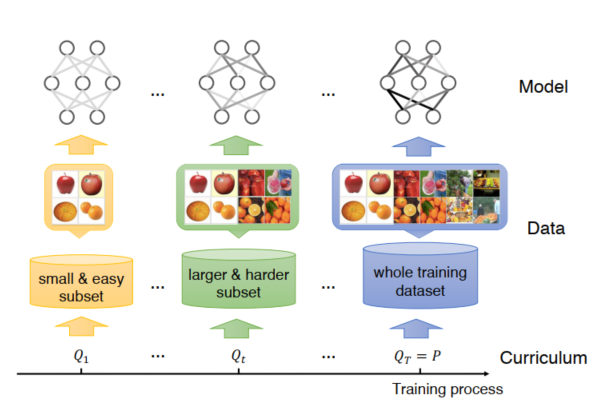
原始的课程学习

课程式学习是在 $T$ 个训练步骤上的训练标准序列 $\mathcal{C}=\left\langle Q_{1}, \ldots, Q_{t}, \ldots, Q_{T}\right\rangle$ ，每个准则 $Q_t$ 是目标训练分布 $P(z)$ 的权重。该准则包括数据/任务、模型容量、学习目标等。满足的准则：

熵增（harder）、权重增加、最后的目标训练分布达到 $P(z)$

从数据层面泛化的课程学习（data level）

在T步内对于training target分布赋权学习。
更加泛化的课程学习（criteria ）

存在“hard to easy”效果更好的examples，为了让课程学习定义更加泛化。提出课程学习是在每一个 $Q_t$ 利用机器学习的所有元素进行训练的设计，比如data、目标函数等。

有效性分析：

1. 模型优化角度

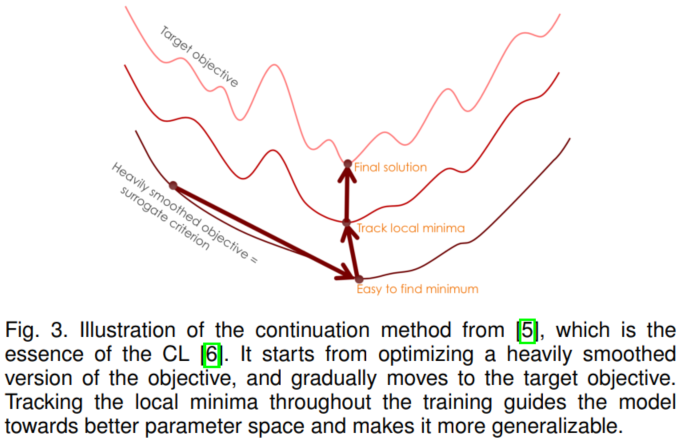
CL可以看成是一种特殊的 continuation 方法（continuation method是一种思想,就是不能一口吃个胖子,一步一步的解决问题。）。这种方法首先优化比较smooth的问题，然后逐渐优化到不够smooth的问题。如下图所示，continuation 方法提供了一个优化目标序列，从一个比较平滑的目标开始，很容易找到全局最小值，并在整个训练过程中跟踪局部最小值。另外，从更容易的目标中学习到的局部最小值具有更好的泛化能力，更有可能近似于全局最小值。

2. 数据分布角度（降噪denoising）

训练分布和测试分布之间存在着由噪声/错误标注的训练数据引起的偏差。直观地讲，训练分布和目标（测试）分布有一个共同的大密度高置信度标注区域，这对应于CL中比较容易的样本。如下图所示，波峰附近的数据代表高置信度的数据即干净的数据，两边（尾部）代表的是低置信度的数据即噪声数据。左图看出，训练数据 $P_{train}$ 比目标数据 $P_{target}$ 噪声更多（其分布尾巴更翘）；右图看出，CL通过加权，一开始分配给噪声数据较小的权重，后面慢慢才给这些数据增加权重。通过这种方式，CL就可以减少来自负样本的影响。

另外，CL本质上是将目标分布下的预期风险上界最小化，这个上界表明，我们可以通过CL的核心思想来处理将 $P_{target(x)}$ 上的预期风险最小化的任务：根据课程设置逐步抽取相对容易的样本，并将这些样本的经验风险最小化。

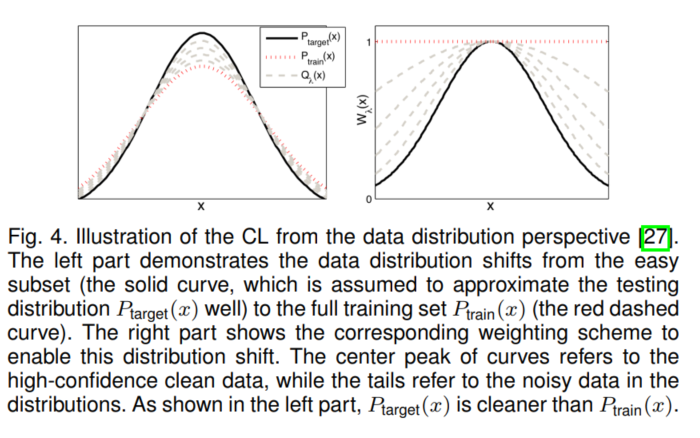
左图为数据分布图；右图为加权后的数据分布图

应用场景

从动机上看，主要分为的是指导训练和降噪。

指导训练：让训练可行/更好。应用：sparse reward RL, multi-task learning, GAN training, NAS（提高效率）;domain adaption, imbalanced classification（让训练可行）
denoise：加速训练、让训练更泛化和鲁棒（针对噪声多的或是异质数据）。应用：weakly-supervised or unsupervised learning, NLP tasks (neural machine translation, natural language understanding, etc.)

方法总结：

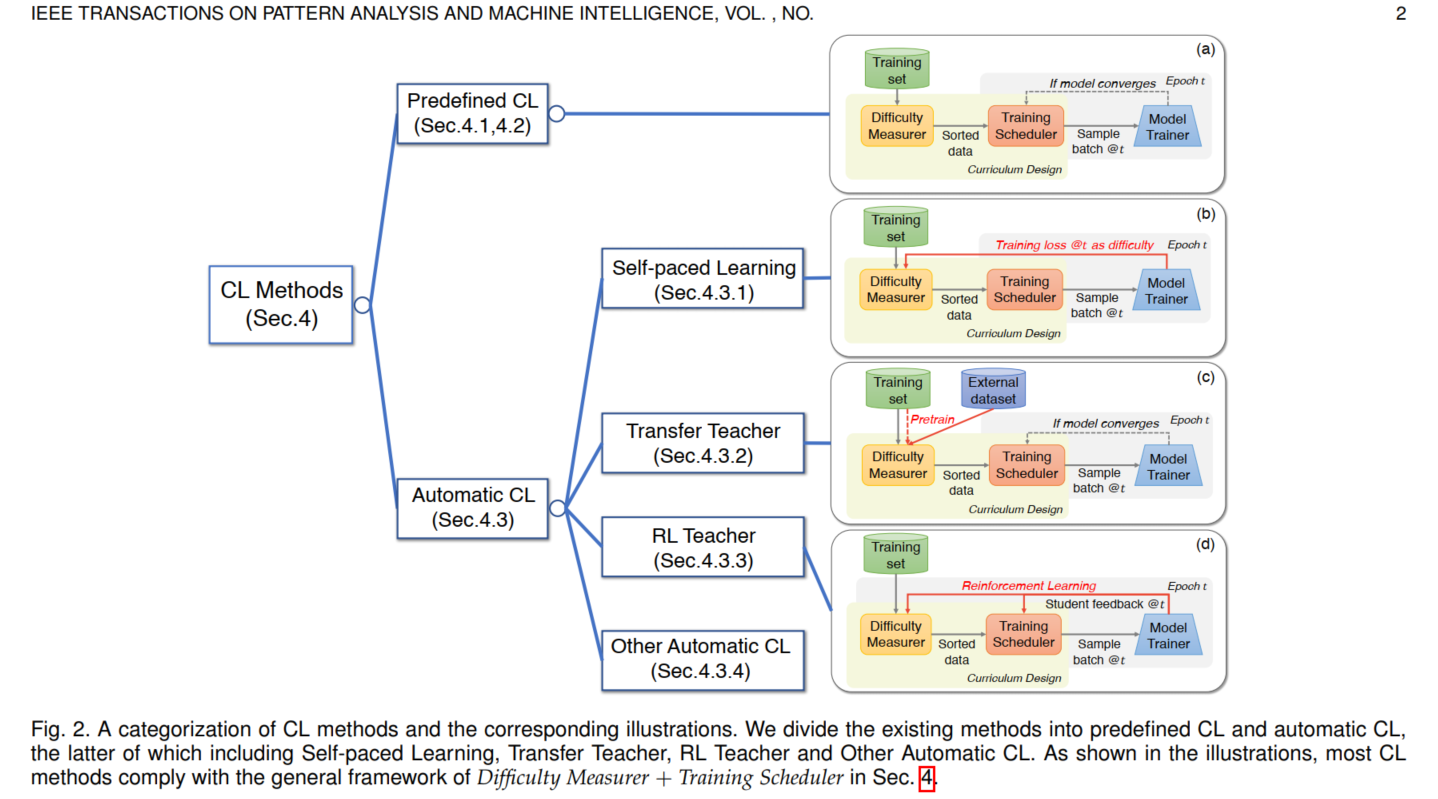
课程学习的核心问题是得到一个ranking function，该函数能够对每条数据/每个任务给出其learning priority (学习优先程度)。这个则由难度测量器（Difficulty Measurer）实现。另外，我们什么时候把 Hard data 输入训练以及每次放多少呢？这个则由训练调度器（Training Scheduler）决定。因此，目前大多数CL都是基于"难度测量器+训练调度器 "的框架设计。根据这两个是否自动设计可以将CL分成两个大类即 Predefined CL 和 Automatic CL。

Predifined CL 的难度测量器和训练调度器都是利用人类先验先验知识由人类专家去设计；而Automatic CL是以数据驱动的方式设计。

1. Predefined CL

1.1 预定义的难度测量器

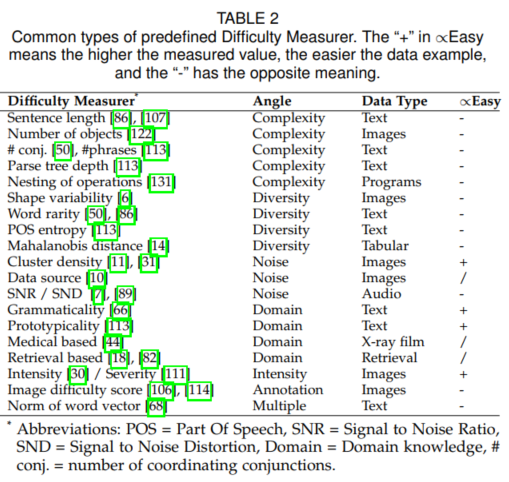
complexity：structural complexity （如句子的长度等）

diversity ：分布的多样性（例如用信息熵来衡量）

noise：噪声角度（如直接从网上爬下的照片噪声就会多）

domain：domain knowledge

IR例子：

[18]Continuation Methods and Curriculum Learning for Learning to Rank(CIKM 2018)

提出了CM和CL两种策略来提升λ-MART的性能。

CM:先针对MSE训练回归森林，然后进行λ-MART训练

CL:需要从训练数据采样。第一种策略根据相关性来划分数据、第二种根据难度进行划分。
[82]Curriculum Learning Strategies for IR An Empirical Study on Conversation Response Ranking (ecir 2020)

1.2 预定义的训练调度器

训练调度器可以分为离散调度器和连续调度器。两者的区别在于：离散型调度器是在每一个固定的次数（>1）后调整训练数据子集，或者在当前数据子集上收敛，而连续型调度器则是在每一个epoch调整训练数据子集。

例子：

离散调度器：

Baby step：排序后分buckets，训练过程逐步引入。

One-Pass ：直接使用下一个bucket，不是引入了。

连续调度器：

设计function$\lambda(t)$得到引入的porpotion。

linear（像linear lr scheduler）：

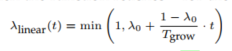
root function：

为了让新加入的samples能够被充分学习，需要让加入的速率降低。

1.3 predifined CL存在的问题

很难预定义CL的方法找到测量器和调度器两者最优的组合。
不够灵活，没有考虑模型自身的反馈在训练过程中。
需要专家知识，代价较高。
人类认为容易的样本对模型来说就不一定容易。（人和机器模型的决策边界不一定一致）

2. Automatic CL

与predifined CL对比：

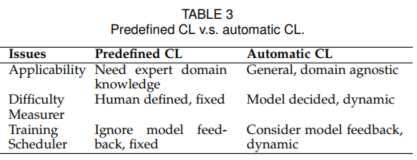
自动CL的方法论分为四类，即Self-paced Learning、Transfer Teacher、RL Teacher 和 其他自动CL。

Automatic CL的分类

2.1 Self-paced Learning

Self-paced Learning 让学生自己充当老师，根据其对实例的损失来衡量训练实例的难度。这种策略类似于学生自学：根据自己的现状决定自己的学习进度。主要利用基于loss的difficulty measurer，有很强的泛化能力。

原始loss，总共N个样本:

$\operatorname*{min}_{w}\mathbb{E}(w;\lambda)\sum_{i=1}^{\mathcal{N}}l_{i}+R(w)$

SPL引入了spl-regularization，v是一系列的weights：

$\operatorname*{min}_{w;v\in[0,1]^{N}}\mathbb{S}\bigl(w,v;\lambda\bigr)\sum_{i=1}v_{i}l_{i}+g\bigl(v;\lambda\bigr).$

SPL原始的l1正则项：

$g(v;\lambda)=-\lambda\sum_{i=1}^{N}v_{i}.$

固定w，我们可以得到最优的v（Eq.9）：

$v_{i}^{\star}=\arg\operatorname*{min}_{v_{i}\in[0,1]}v_{i}l_{i}^{\bigtriangledown}+g(v_{i};\lambda),\quad i=1,2,\cdot\cdot\cdot\cdot,n$

同样固定v,可以优化w(Eq.10）：

$w^{*}=\arg\operatorname*{min}_{w}\sum_{i=1}^{N}v_{i}^{*}l_{i}.$

常见的regularizer:

2.2 Transfer Teacher

SPL在学习初期，学生网络可能是不够成熟的，所以会影响到后面的训练

Transfer Teacher 则通过1个强势的教师模型来充当教师，根据教师对实例的表现来衡量训练实例的难度。教师模型经过预训练，并将其知识转移到测量学生模型训练的例子难度上。

2.3 RL Teacher

RL Teacher 采用强化学习（RL）模式，教师根据学生的反馈，实现数据动态选择。这种策略是人类教育中最理想的场景，教师和学生通过良性互动共同提高：学生根据教师选择的量身定做的学习材料取得最大的进步，而教师也有效地调整自己的教学策略，更好地进行教学。

2.4 其他自动 CL

除上述方法外，其他自动CL方法包括各种自动CL策略。如采取不同的优化技术来自动寻找模型训练的最佳课程，包括贝叶斯优化、元学习、hypernetworks等。

未来研究方向：

评价数据集和指标

虽然各种CL方法已经被提出并被证明是有效的，但很少有工作用通用基准来评估它们。在现有的文献中，数据集和指标在不同的应用中是多样化的。

2. 更完善的理论分析

现有的理论分析为理解CL提供了不同的角度。尽管如此，我们还需要更多的理论来帮助我们揭示为什么典型的CL是有效的。

3. 更多的CL算法以及应用

自动CL为CL在更广泛的研究领域提供了潜在的应用价值，已经成为一个前沿方向。因此，一个很有前途的方向是设计更多的自动CL方法，这些方法可具有不同的优化方式(如：bandit 算法、元学习、超参数优化等)和不同的目标(如：数据选择/加权、寻找最佳损失函数或假设空间等)。除了方法之外，还应该探索CL在更多领域中的应用。

总结：

这篇主要做了以下三项工作：

总结了现有的基于 "难度测量器+训练调度器 "总体框架的CL设计，并进一步将自动CL的方法论分为四类，即Self-paced Learning、Transfer Teacher、RL Teacher 和 其他自动CL。
分析了选择不同CL设计的原则，以利于实际应用。
对连接CL和其他机器学习概念(包括转移学习、元学习、持续学习和主动学习等)的关系的见解，然后指出CL的挑战以及未来潜在的研究方向，值得进一步研究。

Sampling

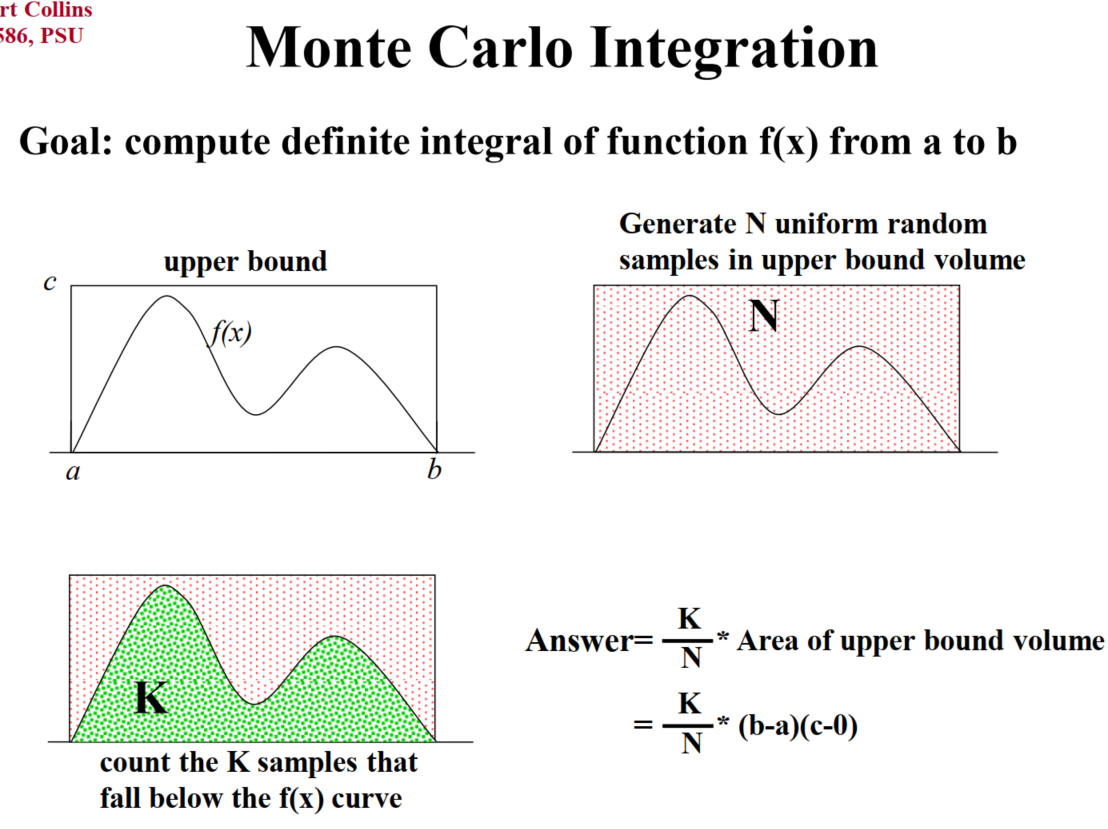
mote carlo integration：求定积分

Inverse Transform Sampling ：

利用cdf:$F(x) = P(X \le x)$

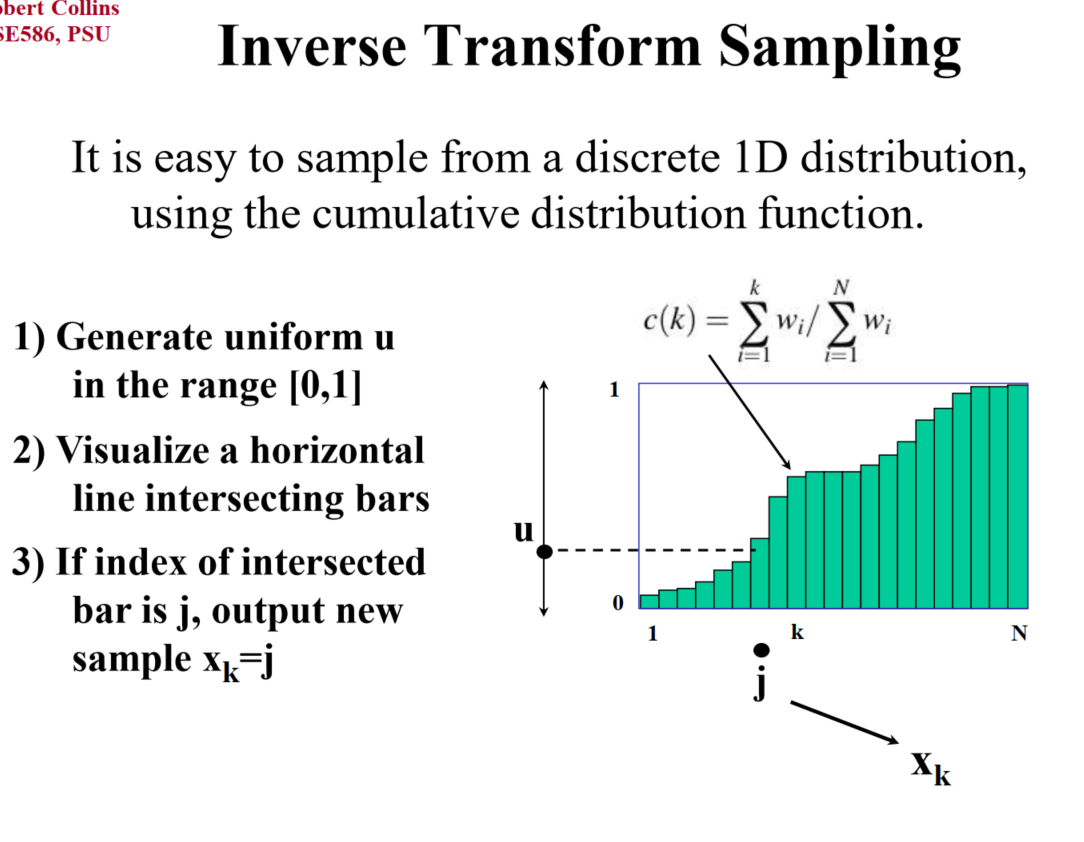
算法：

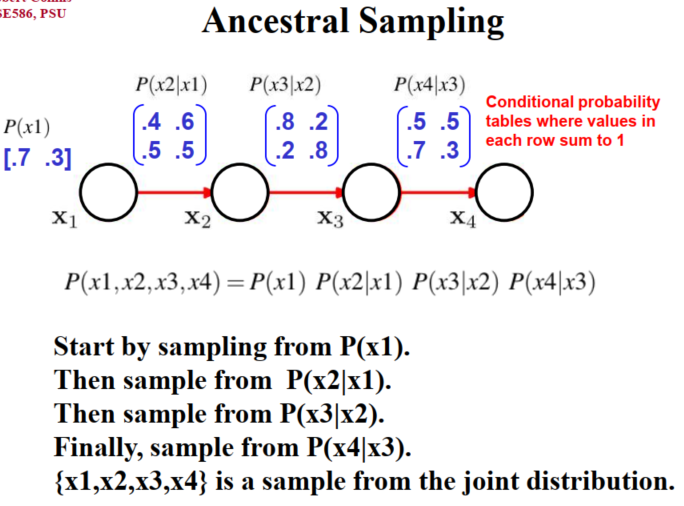
Ancestral sampling（祖先采样）得到联合概率：

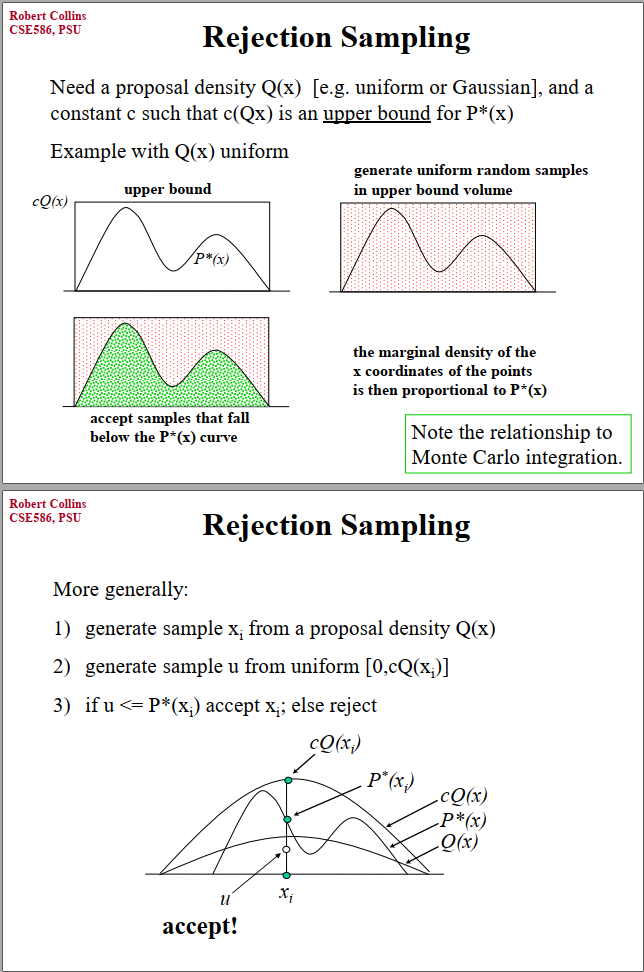
拒绝采样（rejection sampling）：

利用比较容易采样的分布，罩住需要采样分布；

重要性采样（importance sampling）：

不是采样方法，而是快速得到函数期望。依然从容易采样的Q入手，通过权重进行调整。

可以利用重要性采样的w进行重采样：

如果使用拒绝采样、重要性采样，尽量保证proposal distribution是heavy tail的，如果Q密度为0时，P还有密度，那么基本上采样效率会很低（找相近的分布采样效率会高）。

EM and GMM

https://blog.csdn.net/weixin_43661031/article/details/91358990

EM 算法

EM算法是一种迭代算法，1977年Dempster等人总结，用于含有因变量的概率模型极大似然估计，或者最大后验估计。有两步，E步求期望，M步求极大。

Q函数：完全对数似然在给定观测数据Y以及当前$\theta^{(i)}$的情况下对Z的期望。

$Q(\theta, \theta^{(i)}) = E_Z [\log P(Y,Z|\theta)|Y,\theta^{(i)}]$

$_{z(i)}Q^{i}(z{(i)})=1 $

$Q^{i}(z^{(i)})\geq0$

步骤

分为E步和M步，即求Q函数，极大化Q函数。

输入：观测数据Y，隐变量数据Z，联合分布，条件分布；

输出：模型参数。

选取参数的初始值在$\theta^{(0)}$（可任意选择，但是算法对初始值敏感)；开始迭代；
E步：计算
M步：最大化$Q(\theta, \theta^{(i)})$,得到$\theta^{(i+1)}$：

^{(i+1)}=Q(, ^{(i)})
重复2. 3.，直到收敛

停止迭代的条件：或

导出

给定观测数据Y，目标是极大化观测数据（不完全数据）Y关于参数的对数似然函数，即

L()=P(Y|)=_{Z}P(Y,Z|)={ _Z P(Y|Z,) P(Z|)}

其中表示在模型参数为时，观测数据Y的概率分布。

$\begin{align*} P(Y|\theta)&=\sum_Z P(Y,Z|\theta)=\sum_Z P(Z|\theta)P(Y|Z,\theta)\\ \end{align*}$

EM算法通过逐步迭代来逐步近似极大化。假设第i次迭代后的估计值为。下一轮的估计值要使。故

L()-L(^{(i)} )={ _Z P(Y|Z,)P(Z|) }-P(Y|^{(i)} )

利用Jensen不等式（这里用的是$log{\bigl(}\sum_{i=1}^{M}\lambda_{i}x_{i}{\bigr)}\leq\sum_{i=1}^{M}\lambda_{i}log{\bigl(}x_{i}{\bigr)}$）得到下界：

\[\begin{align*} L(\theta)-L(\theta^{(i)} ) &=\log \left\{ \sum_Z P(Y|Z,\theta^{(i)} ) \frac{P(Y|Z,\theta) P(Z|\theta)}{P(Y|Z,\theta^{(i)} )} \right \} - \log P(Y|\theta^{(i)} ) \\ &\geq \sum_Z P(Z|Y,\theta^{(i)} )\log \frac{P(Y|Z,\theta) P(Z|\theta)}{P(Z|Y,\theta^{(i)})} - \log P(Y|\theta^{(i)})\\ &= \sum_Z P(Z|Y,\theta^{(i)} )\log \frac{P(Y|Z,\theta) P(Z|\theta)}{P(Z|Y,\theta^{(i)})} - \sum_ZP(Z|Y,\theta^{(i)} ) \log P(Y|\theta^{(i)}) \\ &= \sum_Z P(Z|Y,\theta^{(i)} )\log \frac{P(Y|Z,\theta) P(Z|\theta)}{P(Z|Y,\theta^{(i)}) P(Y|\theta^{(i)})} \\ \end{align*}\]

令

B(, ^{(i)})=L({(i)})+_Z P(Z|Y,^{(i)} )

是的一个下界。任何可使增大的，都可以使增加。选择能使当前极大的作为新的值。

\[\begin{align*} \theta^{(i+1)} &=\arg \max (L(\theta^{(i)})+\sum_Z P(Z|Y,\theta^{(i)} )\log \frac{P(Y|Z,\theta) P(Z|\theta)}{P(Z|Y,\theta^{(i)}) P(Y|\theta^{(i)})}) \\ &=\arg \max (\sum_Z P(Z|Y,\theta^{(i)}))\log (P(Y|Z,\theta)P(Z|\theta))\\ &=\arg \max (\sum_Z P(Z|Y,\theta^{(i)})\log(P(Y,Z|\theta))) \\ &=\arg \max Q(\theta, \theta^{(i)}) \end{align*}\]

所以EM算法就是通过迭代不断求Q函数，并将之极大化，直至收敛。下图为EM算法的直观解释，是的一个下界。

我们首先初始化模型的参数，我们基于这个参数对每一个隐变量进行分类，此时相当于我们观测到了隐变量。有了隐变量的观测值之后，原来含有隐变量的模型变成了不含隐变量的模型(以上是E步)，因此我们可以直接使用极大似然估计来更新模型的参数（M步），再基于新的参数开始新一轮的迭代，直到参数收敛。

收敛性

定理一：为观测数据的似然函数，是EM算法得到的参数估计序列，是对应的似然函数序列，则是单调递增的。

定理二：是观测数据的对数似然函数，是EM算法得到的参数估计序列，是对应的对数似然函数序列。如果有上界，则收敛到某一值；在函数与满足一定条件下，EM算法得到的参数估计序列的收敛值是的稳定点。

GMM混合高斯

模型定义：

$p(x)=\sum_{k=1}^{K}\alpha_{k}\mathcal{N}(x|\mu_{k},\Sigma_{k})$

$\sum_{k=1}^{K}\alpha_{k}=1$

多个高斯模型的加权平均；（单个表达能力不够）
混合：隐变量->属于哪一个高斯分布

参数学习

$\gamma_{j k}$代表第j个观测来源于k个分模型（01随机变量）---------这里的隐变量

写出完全对数似然

$\begin{aligned} P(y, \gamma \mid \theta) &=\prod_{j=1}^{N} P\left(y_{j}, \gamma_{j 1}, \gamma_{j 2}, \cdots, \gamma_{j K} \mid \theta\right) \\ &=\prod_{k=1}^{K} \prod_{j=1}^{N}\left[\alpha_{k} \phi\left(y_{j} \mid \theta_{k}\right)\right]^{\gamma_{k}} \\ &=\prod_{k=1}^{K} \alpha_{k}^{n_{k}} \prod_{j=1}^{N}\left[\phi\left(y_{j} \mid \theta_{k}\right)\right]^{\gamma_{k}} \\ &=\prod_{k=1}^{K} \alpha_{k}^{n_{k}} \prod_{j=1}^{N}\left[\frac{1}{\sqrt{2 \pi} \sigma_{k}} \exp \left(-\frac{\left(y_{j}-\mu_{k}\right)^{2}}{2 \sigma_{k}^{2}}\right)\right]^{\gamma_{k t}} \end{aligned}$

对数似然：

$\log P(y,\gamma\vert\theta)=\sum_{k=1}^{K}[n_{k}\log\alpha_{k}+\sum_{j=1}^{N}\gamma_{k}\biggl[\log(\frac{1}{\sqrt{2\pi}})-\log\sigma_{k}-\frac{1}{2\sigma_{k}^{2}}(y_{j}-\mu_{k})^{2}\biggr]]$

其中：$n_k = \sum_{j=1}^{N}\gamma_{jk}$, $\sum_{k=1}^{K}n_{k}=N$ （Q函数推导的时候代入）
确定Q函数

$\begin{aligned} Q\left(\theta, \theta^{(i)}\right) &=E\left[\log P(y, \gamma \mid \theta) \mid y, \theta^{(i)}\right] \\ &=E\left\{\sum_{k=1}^{K} [n_{k} \log \alpha_{k}+\sum_{j=1}^{N} \gamma_{j k}\left[\log \left(\frac{1}{\sqrt{2 \pi}}\right)-\log \sigma_{k}-\frac{1}{2 \sigma_{k}^{2}}\left(y_{j}-\mu_{k}\right)^{2}\right]]\right\} \\ &=\sum_{k=1}^{K}\left\{\sum_{j=1}^{N}[\left(E \gamma_{j k}\right) \log \alpha_{k}+\sum_{j=1}^{N}\left(E \gamma_{j k}\right)\left[\log \left(\frac{1}{\sqrt{2 \pi}}\right)-\log \sigma_{k}-\frac{1}{2 \sigma_{k}^{2}}\left(y_{j}-\mu_{k}\right)^{2}\right]]\right\} \end{aligned}$

需要计算期望$E (\gamma_{j k}|y, \theta)$

$\hat{\gamma}_{j k} &=E\left(\gamma_{j k} \mid y, \theta\right)=P\left(\gamma_{j k}=1 \mid y, \theta\right) \\ &=\frac{P\left(\gamma_{j k}=1, y_{j} \mid \theta\right)}{\sum_{k=1}^{K} P\left(\gamma_{j k}=1, y_{j} \mid \theta\right)}&=\frac{P\left(y_{j} \mid \gamma_{j k}=1, \theta\right) P\left(\gamma_{j k}=1 \mid \theta\right)}{\sum_{k=1}^{K} P\left(y_{j} \mid \gamma_{j k}=1, \theta\right) P\left(\gamma_{j k}=1 \mid \theta\right)} &=\frac{\alpha_{k} \phi\left(y_{j} \mid \theta_{k}\right)}{\sum_{k=1}^{K} \alpha_{k} \phi\left(y_{j} \mid \theta_{k}\right)}, \quad j=1,2, \cdots, N ; \quad k=1,2, \cdots, K$

Q函数为：

$Q\left(\theta, \theta^{(i)}\right)=\sum_{k=1}^{K} [n_{k} \log \alpha_{k}+\sum_{k=1}^{N} \hat{\gamma}_{j k}\left[\log \left(\frac{1}{\sqrt{2 \pi}}\right)-\log \sigma_{k}-\frac{1}{2 \sigma_{k}^{2}}\left(y_{j}-\mu_{k}\right)^{2}\right]]$
确定M步

这一步求Q函数对$\theta$的极大值，分别对$\mu \space \sigma \space \alpha$求偏导等于零（$\alpha$需要在满足和为1，所以除个N）解得

${\hat{\mu}}_{k}={\frac{\sum_{j=1}^{N}{\hat{\gamma}}_{k}y_{j}}{\sum_{j=1}^{N}{\hat{\gamma}}_{k}}}$

$\hat{\sigma}_{k}^{2}=\frac{\sum_{j=1}^{N} \hat{\gamma}_{j k}\left(y_{j}-\mu_{k}\right)^{2}}{\sum_{j=1}^{N} \hat{\gamma}_{j k}}$

$\hat{\alpha}_{k}=\frac{n_{k}}{N}=\frac{\sum_{j=1}^{N} \hat{\gamma}_{j k}}{N}$

整体算法：

VI与EM算法关系

https://zhuanlan.zhihu.com/p/97284299

Variational inference （变分推断，以下简称VI）和Expectation maximization（期望极大化，以下简称EM）这两种算法实际上是密切相关的。实际上我们可以将EM看作VI的特殊形式。

对于 $z \rightarrow x$ ，我们有 $p(x,z;\theta) = p(x|z;\theta)p(z;\theta)$ 。如果我们想根据 $x$ 推测隐变量 $z$ 的概率，我们就需要计算如下的积分： $p(z|x;\theta) = \frac{p(x,z;\theta)}{\int dz\ p(x,z;\theta)}$ 。然而 $\int dz\ p(x,z;\theta)$ 有时难以计算，尤其是对于高维的系统，因为高维系统里面的积分复杂度很高。因此我们需要发展一种更加方便的方法来近似表达 $p(z|x;\theta)$ 。VI就是用函数 $q(z)$ 来近似表达 $p(z|x;\theta)$

Jensen's inequality

对于任何的凸函数（convex function） $f(x)$ ，我们都有 $\mathbb{E}(f(x))\geq f(\mathbb{E}(x))$ 。Fig 1是一个直观的特例，当自变量 $X$ 的分布是在 $a，b$ 两点的均匀分布的时候，从图中可以明显看出 $\mathbb{E}(f(X))\geq f(\mathbb{E}(X))$ 。Jensen's inequality $\mathbb{E}(f(x))\geq f(\mathbb{E}(x))$ 取等号的条件是 $x=\mathbb{E}(x)$ ，即 $x$ 是一个常数。

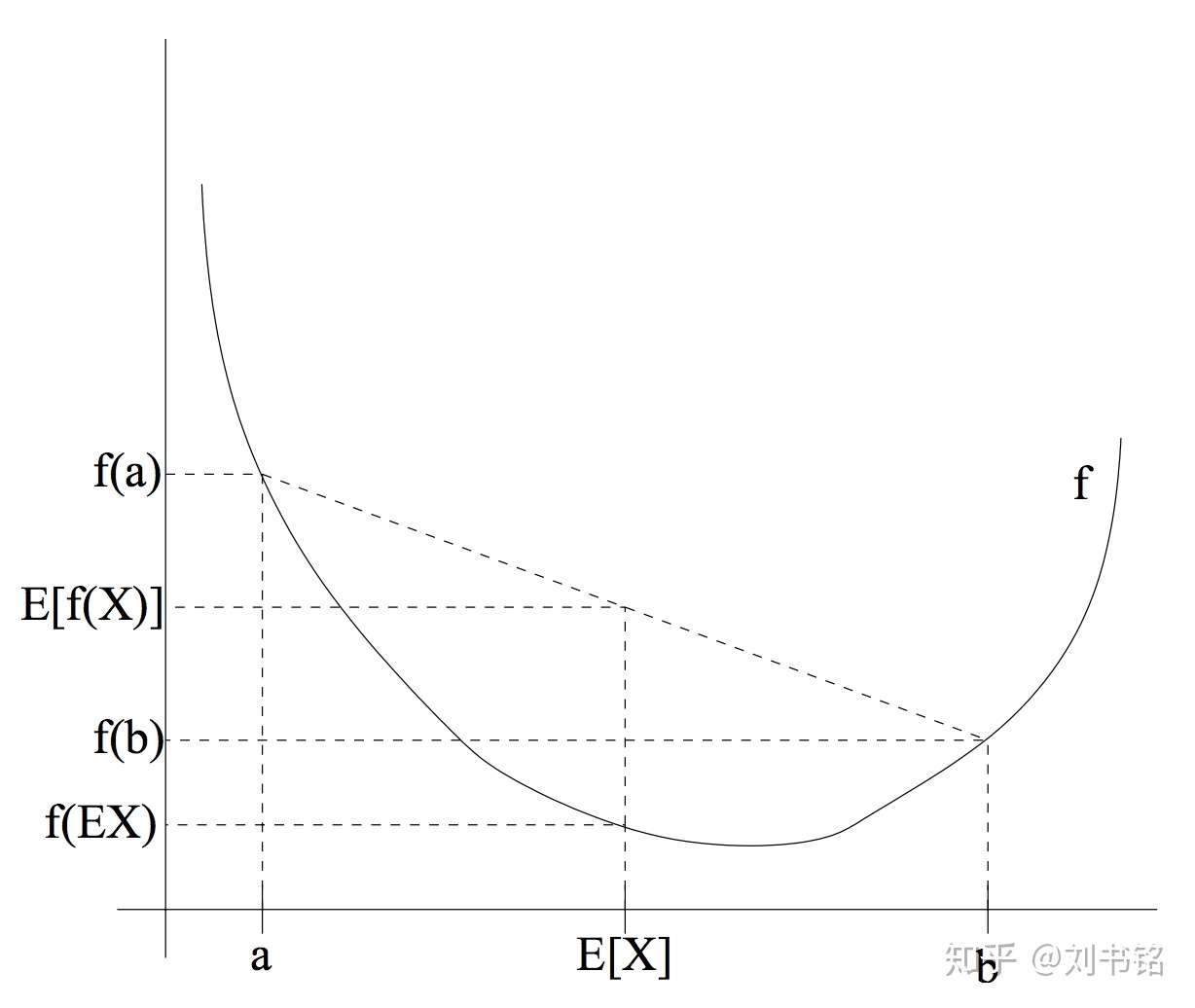Fig 1. 一个凸函数以及E[(f(X))]和f[E(X)]的取值比较，这里X的分布是在a和b两点的均匀分布（图片来自于Andrew Ng的讲义，见Reference &amp;amp;amp;amp;amp;amp;amp;amp; Acknowledgement）

由于 $\log(\cdot)$ 是一个凹函数，即 $-\log(\cdot)$ 是一个凸函数，所以满足 $\mathbb{E}(\log(x))\leq \log(\mathbb{E}(x))$ ，取等号的条件是自变量 $x$ 是一个常数。之后我们要用到有关 $\log(\cdot)$ 的这些性质。

KL divergence & ELBO

先证明一个数学结论：对于任意的概率 $p(x;\theta)$ （ $x$ 是变量， $\theta$ 是参数）， $\forall \ q(z)$ （这里 $q(z)$ 是某个关于 $z$ 的概率密度函数），我们有

其中的不等号来自于Jensen's inequality应用在凹函数 $\log(\cdot)$ 上的结论。由此我们知道，对于上面的式子取等号的条件是 $p(x,z;\theta) \propto q(z)$ （也就是说在给定 $x$ 的情况下二者的比例是一个常数，无论 $z$ 取什么值），所以取等号的时候 $q(z) = \frac{p(x,z;\theta)}{\int dz\ p(x,z;\theta)}=p(z|x;\theta)$ （这是由于 $q(z)$ 是概率密度，因此满足归一化条件）。由此我们可以定义KL divergence（记为 $J_{KL}(x;\theta)$ ）和Evidence Lower BOund（简称为ELBO，记为 $L(x;\theta)$ ）：

由此可见KL divergence一定非负，而ELBO是 $\log p(x;\theta)$ 的下界。KL divergence最小的时候等于0，此时 $q(z)=p(z|x;\theta)$ ，这是根据Jensen不等式取等号的条件得出的。并且KL divergence越小， $q(z)$ 越接近 $p(z|x;\theta)$ 。减小KL divergence等价于增大ELBO，因为我们要优化的目标函数是 $q(z)$ ，而 $\log P(x;\theta)$ 可以看作给定的量。

由此我们得到一个重要的结论：优化 $q(z)$ 来增大ELBO等价于优化 $q(z)$ 来逼近 $p(z|x;\theta)$ 。

以下我们通过极大化ELBO，从而训练得到一个好的函数 $q(z)$ 来近似表达 $p(z|x;\theta)$ 。我们可以将ELBO的形式等价变换一下，得到另一种等价形式：

其中 $S(q(z)) = - \int dz\ q(z)\log q(z)$ 是著名的Gibbs entropy。

Variational Inference

在实际操作中，首先我们有已经观察到的 $N$ 个数据点 $x_i\ (i=1,\cdots,N)$ ，我们需要通过优化 $q_i$ 来极大化ELBO，即对于每个数据点 $x_i$ ，我们希望得到函数 $q_i(z) \approx p(z|x_i;\theta)$ 。每个 $x_i$ 对应的ELBO是

我们的目标是极大化 $\sum_{i=1}^N L(x_i;\theta,q_i)$ ：

注意到对于不同的 $x_i$ ，我们选取的函数形式 $q_i(z)$ 不同，因为 $p(z|x_i;\theta)$ 在 $x_i$ 不同的时候是不同的关于 $z$ 的函数。一般来说，通过选取合适的、简单的 $q_i(z)$ 的形式，例如exponential family， $S(q_i(z))$ 可以解析地计算出来；对于 $\mathbb{E}_{q_i}[\log p(x_i,z;\theta)]$ 则需要用stochastic optimization进行极大化，从而优化函数 $q_i$ （也就是优化函数 $q_i$ 的表达式里面包含的参数）。总结一下，VI就是通过选取一些形式简单的、具有良好性质的函数 $q(z)$ 来近似表达 $p(z|x;\theta)$ ，具体的操作方法是极大化ELBO。

Expectation Maximization

EM实际上可以看作一个简化的VI（通过一定的适用条件和一个类似于“作弊”的方法来简化计算）。EM的适用条件是函数 $p(z|x_i;\theta)$ 的形式不太复杂，我们可以显式地表达出 $p(z|x_i;\theta)$ 的时候。从适用条件上来看EM就是VI的一个特例。回忆第1节Motivation中我们说过，有时候 $\int dz\ p(x,z;\theta)$ 难以计算，所以难以直接写出 $p(z|x,\theta)$ 的具体形式。而EM就是适用于 $\int dz\ p(x,z;\theta)$ 不难计算的情况，此时我们可以直接写出 $p(z|x,\theta)$ 的具体形式。

当函数 $p(z|x_i,\theta)$ 的形式不太复杂的时候，我们自然会选择 $q_i(z) = p(z|x_i;\theta)$ 来训练，因此我们可以说，EM就是选取 $q_i(z) = p(z|x_i;\theta)$ 的VI，这和EM的适用条件是自洽的。以下首先写出EM的算法，然后指出其中关键的“作弊”一步在哪里。

EM Algorithm

BEGIN

我们有 $N$ 个数据点 $x_i\ (i=1,\cdots,N)$ ，并且我们有函数 $p(x,z;\theta)$ 和 $p(z|x;\theta)$ 的表达式。

Step 0，初始化：初始随机猜测参数 $\theta_0$

Step 1, E-step：在第 $t$ 步的时候 $(t=0,1,\cdots,T)$ ，计算 $p(z|x_i,\theta_t)$

Step2, M-step: 按照如下规则得到新的参数 $\theta_{t+1}$ ：

$\theta_{t+1} = {\rm argmax}_{\theta}\ \sum_{i=1}^N \int dz\ p(z|x_i;\theta_t) \log p(x_i,z;\theta)$

Step3, 重复 Step 1 & 2（迭代）直到收敛。

END

其中关键的“作弊”步骤是Step2，因为*严格来说我们应该这样计算* $\theta_{t+1}$ ：

也就是将 $q_i(z)$ 替换成 $p(z|x_i;\theta)$ 后maximize ELBO。但是*实际上这个算法却是这么做的*：

也就是将ELBO表达式中的某几个 $\theta$ 固定在了 $\theta_t$ 的值（其中 $\theta_t$ 是第 $t$ 次优化得到的参数），只优化其余位置的 $\theta$ 值，从而使得极大化算法更加简便。同时通过迭代方法确保最后能收敛到一个local maximum。由于 $\theta_t$ 相当于常数，因此 $- \int dz\ p(z|x_i;\theta_t)\log p(z|x_i;\theta_t)$ 相当于常数项，在极大化的时候可以去掉，由此我们可以得到

并且通过迭代求解找到 local maximum。