第九次周报

发表于 2022-02-03 更新于 2022-06-28 分类于周报

week 9 内容：

louis philippe morency 《多模态机器学习》 80%
论文阅读：
1. A Survey of Clustering With Deep Learning: From the Perspective of Network Architecture
2. EM、GMM
3. SpectralCoclustering

A Survey of Clustering With Deep Learning: From the Perspective of Network Architecture

近些年来很多研究几种在使用深度神经网络学习更好的表示来提高聚类性能。这篇综述从网络框架的角度进行了研究，他们首先介绍了领域相关知识，然后提出了深度学习进行聚类的相关分类方法（taxonomy），最后提出未来发展的方向并做了总结。

Intorduction

数据聚类是机器学习、模式识别、计算机视觉、数据压缩等领域的一个基本问题。聚类的目标是根据一些相似度量(如欧几里德距离)将相似数据分类成一个聚类传统的聚类方法对高维数据的聚类性能通常很差，这是由于这些方法使用的相似度进行度量的效率较低。此外，这些方法在大规模数据集上通常具有较高的计算复杂度。因此，人们广泛研究降维和特征转换方法，将原始数据映射到一个新的特征空间中，生成的数据更容易被现有的分类器分离。一般来说，现有的数据变换方法包括线性变换如主成分分析(PCA)和等非线性变换如核方法、谱方法等。然而，潜在结构高度复杂的数据仍挑战着现有的聚类方法。深度神经网络(DNNs)由于其固有的高度非线性变换特性，可以将数据转换为更有利于聚类的表示形式。

##### 传统聚类方法分类

基于划分的方法（partition-based）
基于密度的方法（density-based）
层次的方法（hierarchical）
其他

由于深度学习聚类的本质是学习面向聚类的表示，本文基于网络结构进行了分类

深度学习的聚类方法

基于autoencoder：训练解码器和编码器，解码器是训练时候重建回原始数据，编码器是训练的mapping function（降维、非线性表示）
ClusterDNN: 通过特定聚类loss进行约束训练的前馈神经网络
基于GAN和VAE:它们不仅可以执行聚类任务，还可以从获得的聚类中生成新的样本

PRELIMINARIES

结构：

MLP:对聚类任务，好的初始化是必要的，避免训练陷入局部最优
CNN：不需要特定初始化，但良好的初始化能显著提高性能。

clustering loss：

主聚类损失 Principal Clustering Loss：这类聚类损失函数包括样本的聚类中心（cluster centroids）和聚类分配(cluster assignment)。在聚类损耗引导下对网络进行训练后，可以直接得到聚类。
辅助性损失 Auxiliary Clustering Loss：第二类只起到引导网络学习更可行的聚类表示的作用，不能直接输出聚类。这意味着只有辅助聚类损失的深层聚类方法需要在训练完网络后运行一种聚类方法才能得到聚类。

metrics:

聚类准确率：

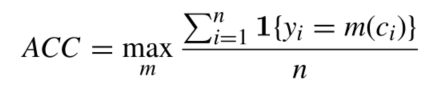
\[A C C=\operatorname*{max}_{m}{\frac{\int_{i=1}^{n}\sum\{y_{i}=m(c_{i})\}}{n}}\]

c是聚类分配，y是ground truth， m是mapping function

Normalized Mutual Information(NMI)

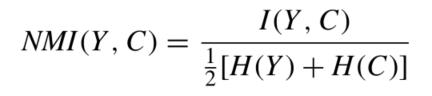
I是互信息，H是信息熵

深度聚类方法

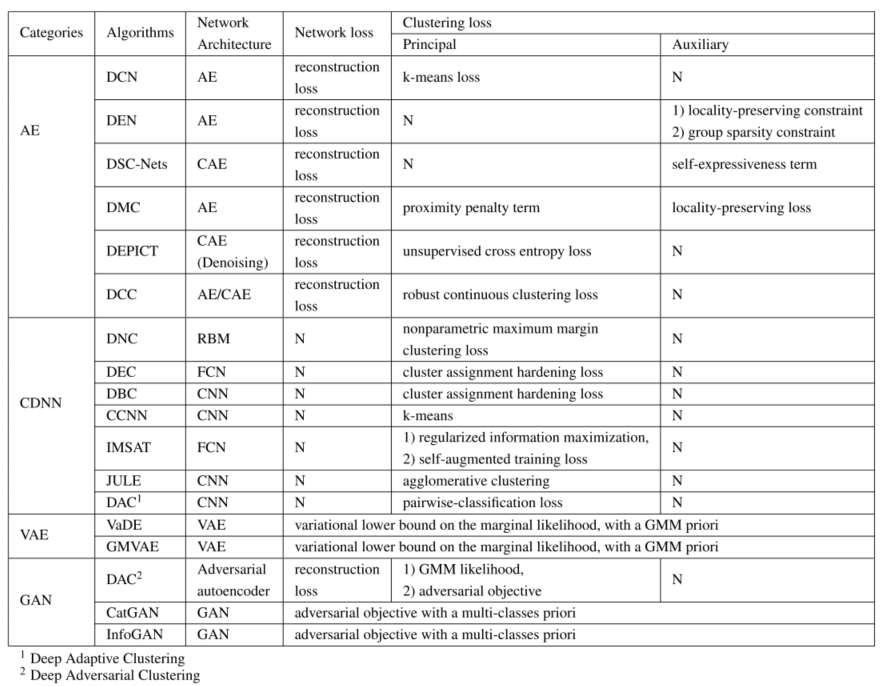
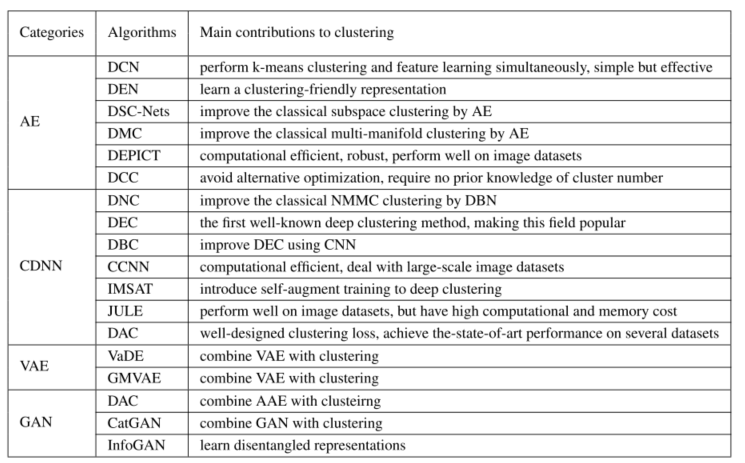
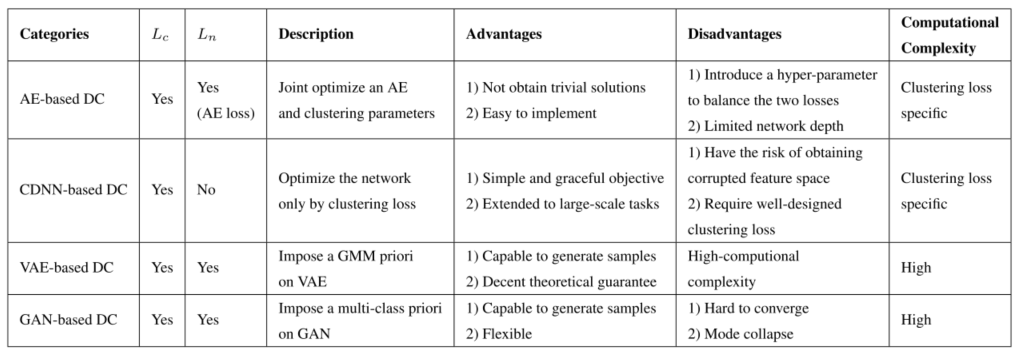
深度聚类方法的损失函数(优化目标)通常由网络损失Ln和聚类损失Lc两部分组成：

\[{\cal L}=\lambda L_{n}+(1-\lambda)L_{c}\]

Ln:网络损失可以是自动编码器(AE)的重构损失、变分自编码器(VAE)的变分损失或生成式对抗网络(GAN)的对抗损失。

Lc：群体之间特征区分更明显

AE based

reconstruction loss：

\(\operatorname*{min}_{\phi,\theta}{\cal L}_{r e c}=\operatorname*{min}_{\bigl|n\bigr|}\sum_{i=1}^{n}\left|\left|\,x_{i}-g_{\theta}(f_{\phi}(x_{i})\right\gt \right|^{2}\)

total loss:

\(L=\lambda L_{r e c}+(1-\lambda)L_{t}\)

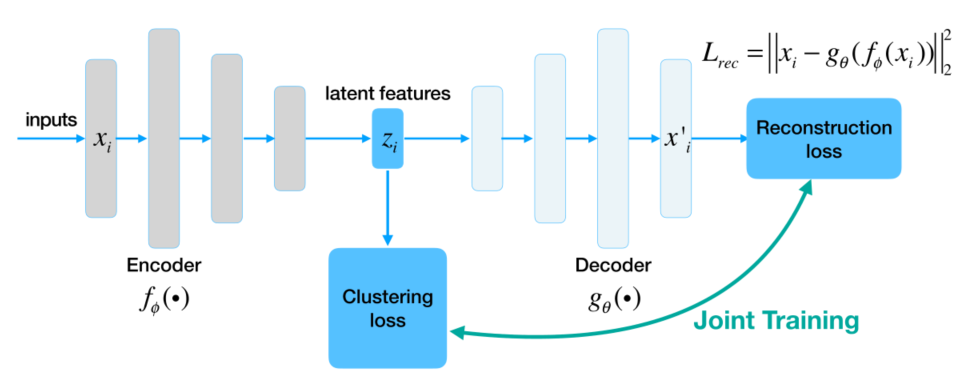
提升性能：
1. 结构：对于含有空间不变性的数据可加入pooling
2. 鲁棒性：为了避免过拟合和提高鲁棒性，在输入中加入噪声
3. 引入特征限制，如正则化
4. 把各层的重构损失都加入到loss中
例子：
1. DCN：它结合了自动编码器和k-means算法。首先进行预训练AE，然后联合优化重建损失和k-means损失。
CDNN-Based

没有了reconstruction loss，基于cdn的算法存在获取损坏特征空间的风险，当所有的数据点被简单地映射到紧凑的聚类上时，导致聚类损失值很小，但没有意义。因此，需要仔细设计聚类loss，对于一定的聚类loss，网络初始化很重要。因此，基于cdn的深度聚类算法按照网络初始化的方式分为三类，即无监督预训练、有监督预训练和随机初始化。
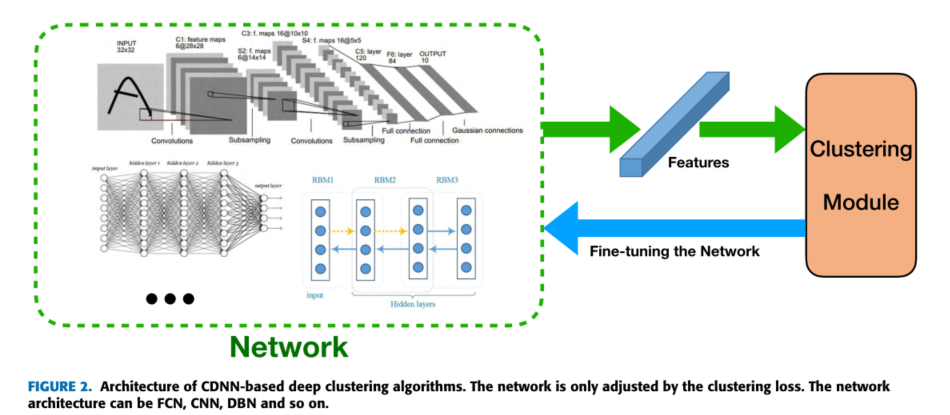
1. unsupervised
  
  这些算法首先以无监督的方式训练RBM或自动编码器，然后通过聚类loss对网络(仅对自动编码器的编码器部分)进行微调。
2. supervised
  
  复杂的图像数据中提取可行的特征（domain pretrain）
3. non pretrain
  
  在精心设计的聚类损失的指导下，网络也可以训练提取判别特征
VAE-BASED

与传统的聚类方法相比，基于ae和cdn的深度聚类方法有了显著的改进。然而，它们是专门为聚类而设计的，不能揭示数据的真正底层结构，这就妨碍了它们扩展到聚类之外的其他任务，例如生成样本。VAE可以被认为是AE的生成变体，因为它强制AE的潜在代码遵循预定义的分布。VAE将变分贝叶斯方法与神经网络的灵活性和可扩展性相结合。
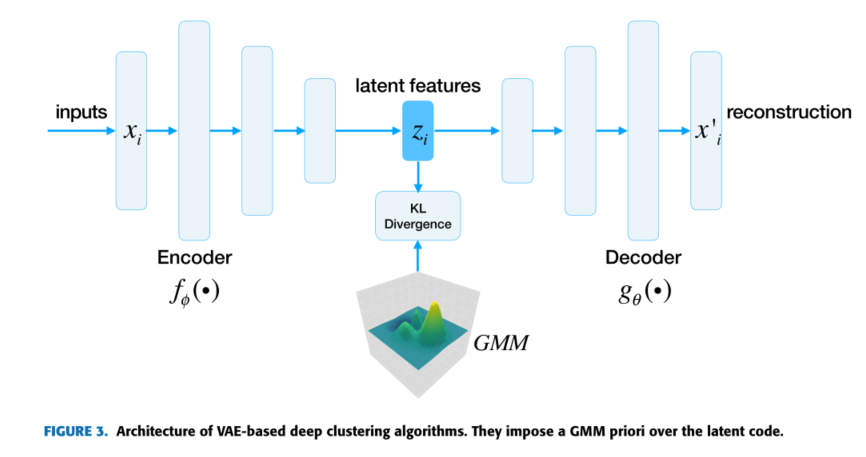
GAN-BASED

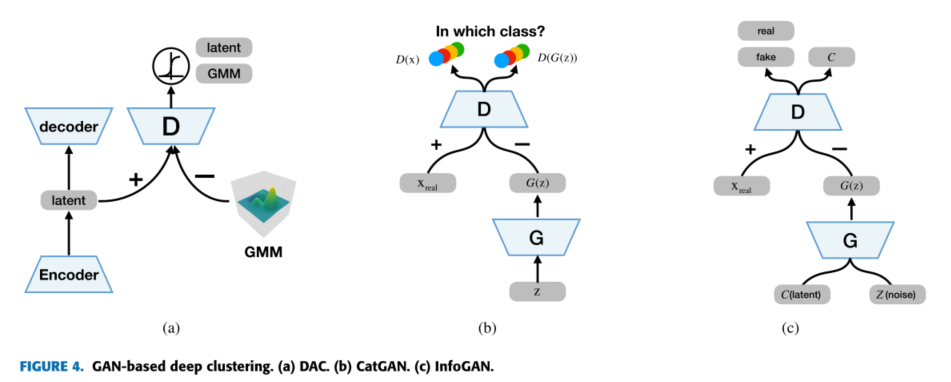
FUTURE OPPORTUNITIES

future opportunities

目前还没有理论分析解释深度学习聚类工作原理以及如何进一步提高聚类性能
其他网络架构与聚类相结合
引入tricks降低训练难度，提高鲁棒性
引入其他任务如多任务学习、迁移学习

EM 算法

EM算法是一种迭代算法，1977年Dempster等人总结，用于含有隐变量的概率模型极大似然估计，或者最大后验估计。有两步，E步求期望，M步求极大。

Q函数：完全对数似然在给定观测数据Y以及当前\(\theta^{(i)}\)的情况下对Z的期望。

\(Q(\theta, \theta^{(i)}) = E_Z [\log P(Y,Z|\theta)|Y,\theta^{(i)}]\)

\(\sum_{z(i)}Q^{i}(z^{(i)}) = 1\)

\(Q^{i}(z^{(i)})\geq0\)

步骤

分为E步和M步，即求Q函数，极大化Q函数。

输入：观测数据Y，隐变量数据Z，联合分布，条件分布；

输出：模型参数。

选取参数的初始值在\(\theta^{(0)}\)（可任意选择，但是算法对初始值敏感)；开始迭代；
E步：计算
M步：最大化\(Q(\theta, \theta^{(i)})\),得到\(\theta^{(i+1)}\)：

^{(i+1)}=Q(, ^{(i)})
重复2. 3.，直到收敛

停止迭代的条件：或

导出

给定观测数据Y，目标是极大化观测数据（不完全数据）Y关于参数的对数似然函数，即

L()=P(Y|)=_{Z}P(Y,Z|)={ _Z P(Y|Z,) P(Z|)}

其中表示在模型参数为时，观测数据Y的概率分布。

\(\begin{align*} P(Y|\theta)&=\sum_Z P(Y,Z|\theta)=\sum_Z P(Z|\theta)P(Y|Z,\theta)\\ \end{align*}\)

EM算法通过逐步迭代来逐步近似极大化。假设第i次迭代后的估计值为。下一轮的估计值要使。故

L()-L(^{(i)} )={ _Z P(Y|Z,)P(Z|) }-P(Y|^{(i)} )

利用Jensen不等式（这里用的是\(log{\bigl(}\sum_{i=1}^{M}\lambda_{i}x_{i}{\bigr)}\leq\sum_{i=1}^{M}\lambda_{i}log{\bigl(}x_{i}{\bigr)}\)）得到下界：

\[\begin{align*} L(\theta)-L(\theta^{(i)} ) &=\log \left\{ \sum_Z P(Y|Z,\theta^{(i)} ) \frac{P(Y|Z,\theta) P(Z|\theta)}{P(Y|Z,\theta^{(i)} )} \right \} - \log P(Y|\theta^{(i)} ) \\ &\geq \sum_Z P(Z|Y,\theta^{(i)} )\log \frac{P(Y|Z,\theta) P(Z|\theta)}{P(Z|Y,\theta^{(i)})} - \log P(Y|\theta^{(i)})\\ &= \sum_Z P(Z|Y,\theta^{(i)} )\log \frac{P(Y|Z,\theta) P(Z|\theta)}{P(Z|Y,\theta^{(i)})} - \sum_ZP(Z|Y,\theta^{(i)} ) \log P(Y|\theta^{(i)}) \\ &= \sum_Z P(Z|Y,\theta^{(i)} )\log \frac{P(Y|Z,\theta) P(Z|\theta)}{P(Z|Y,\theta^{(i)}) P(Y|\theta^{(i)})} \\ \end{align*}\]

令

B(, ^{(i)})=L({(i)})+_Z P(Z|Y,^{(i)} )

是的一个下界。任何可使增大的，都可以使增加。选择能使当前极大的作为新的值。

\[\begin{align*} \theta^{(i+1)} &=\arg \max (L(\theta^{(i)})+\sum_Z P(Z|Y,\theta^{(i)} )\log \frac{P(Y|Z,\theta) P(Z|\theta)}{P(Z|Y,\theta^{(i)}) P(Y|\theta^{(i)})}) \\ &=\arg \max (\sum_Z P(Z|Y,\theta^{(i)}))\log (P(Y|Z,\theta)P(Z|\theta))\\ &=\arg \max (\sum_Z P(Z|Y,\theta^{(i)})\log(P(Y,Z|\theta))) \\ &=\arg \max Q(\theta, \theta^{(i)}) \end{align*}\]

所以EM算法就是通过迭代不断求Q函数，并将之极大化，直至收敛。下图为EM算法的直观解释，是的一个下界。

我们首先初始化模型的参数，我们基于这个参数对每一个隐变量进行分类，此时相当于我们观测到了隐变量。有了隐变量的观测值之后，原来含有隐变量的模型变成了不含隐变量的模型(以上是E步)，因此我们可以直接使用极大似然估计来更新模型的参数（M步），再基于新的参数开始新一轮的迭代，直到参数收敛。

收敛性

定理一：为观测数据的似然函数，是EM算法得到的参数估计序列，是对应的似然函数序列，则是单调递增的。

定理二：是观测数据的对数似然函数，是EM算法得到的参数估计序列，是对应的对数似然函数序列。如果有上界，则收敛到某一值；在函数与满足一定条件下，EM算法得到的参数估计序列的收敛值是的稳定点。

GMM混合高斯

模型定义：

\(p(x)=\sum_{k=1}^{K}\alpha_{k}\mathcal{N}(x|\mu_{k},\Sigma_{k})\)

\(\sum_{k=1}^{K}\alpha_{k}=1\)

多个高斯模型的加权平均；（单个表达能力不够）
混合：隐变量->属于哪一个高斯分布

参数学习

\(\gamma_{j k}\)代表第j个观测来源于k个分模型（01随机变量）---------这里的隐变量

写出完全对数似然

\(\begin{aligned} P(y, \gamma \mid \theta) &=\prod_{j=1}^{N} P\left(y_{j}, \gamma_{j 1}, \gamma_{j 2}, \cdots, \gamma_{j K} \mid \theta\right) \\ &=\prod_{k=1}^{K} \prod_{j=1}^{N}\left[\alpha_{k} \phi\left(y_{j} \mid \theta_{k}\right)\right]^{\gamma_{k}} \\ &=\prod_{k=1}^{K} \alpha_{k}^{n_{k}} \prod_{j=1}^{N}\left[\phi\left(y_{j} \mid \theta_{k}\right)\right]^{\gamma_{k}} \\ &=\prod_{k=1}^{K} \alpha_{k}^{n_{k}} \prod_{j=1}^{N}\left[\frac{1}{\sqrt{2 \pi} \sigma_{k}} \exp \left(-\frac{\left(y_{j}-\mu_{k}\right)^{2}}{2 \sigma_{k}^{2}}\right)\right]^{\gamma_{k t}} \end{aligned}\)

对数似然：

\(\log P(y,\gamma\vert\theta)=\sum_{k=1}^{K}[n_{k}\log\alpha_{k}+\sum_{j=1}^{N}\gamma_{k}\biggl[\log(\frac{1}{\sqrt{2\pi}})-\log\sigma_{k}-\frac{1}{2\sigma_{k}^{2}}(y_{j}-\mu_{k})^{2}\biggr]]\)

其中：\(n_k = \sum_{j=1}^{N}\gamma_{jk}\), \(\sum_{k=1}^{K}n_{k}=N\) （Q函数推导的时候代入）
确定Q函数

\(\begin{aligned} Q\left(\theta, \theta^{(i)}\right) &=E\left[\log P(y, \gamma \mid \theta) \mid y, \theta^{(i)}\right] \\ &=E\left\{\sum_{k=1}^{K} [n_{k} \log \alpha_{k}+\sum_{j=1}^{N} \gamma_{j k}\left[\log \left(\frac{1}{\sqrt{2 \pi}}\right)-\log \sigma_{k}-\frac{1}{2 \sigma_{k}^{2}}\left(y_{j}-\mu_{k}\right)^{2}\right]]\right\} \\ &=\sum_{k=1}^{K}\left\{\sum_{j=1}^{N}[\left(E \gamma_{j k}\right) \log \alpha_{k}+\sum_{j=1}^{N}\left(E \gamma_{j k}\right)\left[\log \left(\frac{1}{\sqrt{2 \pi}}\right)-\log \sigma_{k}-\frac{1}{2 \sigma_{k}^{2}}\left(y_{j}-\mu_{k}\right)^{2}\right]]\right\} \end{aligned}\)

需要计算期望\(E (\gamma_{j k}|y, \theta)\)

\(\hat{\gamma}_{j k} &=E\left(\gamma_{j k} \mid y, \theta\right)=P\left(\gamma_{j k}=1 \mid y, \theta\right) \\ &=\frac{P\left(\gamma_{j k}=1, y_{j} \mid \theta\right)}{\sum_{k=1}^{K} P\left(\gamma_{j k}=1, y_{j} \mid \theta\right)}&=\frac{P\left(y_{j} \mid \gamma_{j k}=1, \theta\right) P\left(\gamma_{j k}=1 \mid \theta\right)}{\sum_{k=1}^{K} P\left(y_{j} \mid \gamma_{j k}=1, \theta\right) P\left(\gamma_{j k}=1 \mid \theta\right)} &=\frac{\alpha_{k} \phi\left(y_{j} \mid \theta_{k}\right)}{\sum_{k=1}^{K} \alpha_{k} \phi\left(y_{j} \mid \theta_{k}\right)}, \quad j=1,2, \cdots, N ; \quad k=1,2, \cdots, K\)

Q函数为：

\(Q\left(\theta, \theta^{(i)}\right)=\sum_{k=1}^{K} [n_{k} \log \alpha_{k}+\sum_{k=1}^{N} \hat{\gamma}_{j k}\left[\log \left(\frac{1}{\sqrt{2 \pi}}\right)-\log \sigma_{k}-\frac{1}{2 \sigma_{k}^{2}}\left(y_{j}-\mu_{k}\right)^{2}\right]]\)
确定M步

这一步求Q函数对\(\theta\)的极大值，分别对\(\mu \space \sigma \space \alpha\)求偏导等于零（\(\alpha\)需要在满足和为1，所以除个N）解得

\({\hat{\mu}}_{k}={\frac{\sum_{j=1}^{N}{\hat{\gamma}}_{k}y_{j}}{\sum_{j=1}^{N}{\hat{\gamma}}_{k}}}\)

\(\hat{\sigma}_{k}^{2}=\frac{\sum_{j=1}^{N} \hat{\gamma}_{j k}\left(y_{j}-\mu_{k}\right)^{2}}{\sum_{j=1}^{N} \hat{\gamma}_{j k}}\)

\(\hat{\alpha}_{k}=\frac{n_{k}}{N}=\frac{\sum_{j=1}^{N} \hat{\gamma}_{j k}}{N}\)