第十次周报

发表于 2022-02-11 更新于 2022-06-28 分类于周报

week 10 内容：

louis philippe morency 《多模态机器学习》 90%
kaggle fashion recommendation competition:
1. 完成EDA、数据预处理
2. 用流行度、item相关性、最近购买的item三种方法，进行了提交（baseline）
论文阅读：
1. BGSP、BKM聚类
2. fashion recommendation相关
3. boosting相关（待完善）

1 Co-clustering

Bipartite spectral graph partition（BGSP）-SpectralCoclustering（2001）

https://scikit-learn.org/stable/modules/biclustering.html#spectral-biclustering

共同聚类，也称为双聚类，该方法在数据矩阵中同时聚类样本集和特征集。由于同时利用了样本类群和特征类群之间的关系，该方法相比传统聚类性能更优异。受互联网技术发展的影响，共聚类已成为近年来数据挖掘领域的一个研究热点。从分类角度，共聚类有两种类型：

棋盘格形式的共聚类：如下图，聚类完成后矩阵呈现棋盘格形式，该方法假设数据矩阵中每一个元素都属于一个共聚类簇。
对角共聚类：如下图，聚类完成后类簇位于矩阵对角线上，该方法仅考虑数据中的部分数据形成共聚类簇。

对于很多有着稀疏矩阵的应用来说，对角共聚类往往是更好的选择。一方面，对于棋盘格式的共聚类而言，稀疏矩阵中大部分的条目是为0的，对于共聚类没有贡献。另一方面，在实际的应用中，数据矩阵往往掺杂着许多噪声，这些噪声极大第降低了共聚性能。

在基于对角的共聚类方法中，最著名的是二部谱图划分(BSGP)方法(较快)。然而，由于BSGP在求解过程中涉及奇异值分解，因此在计算上无法用于大型数据集，这严重限制了BSGP在实际应用中的范围。此外，BSGP基于谱图的双分区Ncuts。在处理多分区问题时，首先需要将原离散问题放宽为一个连续问题，然后使用k-means算法输出离散结果。在这种离散-连续-离散变换过程中，最终得到的优化问题与BSGP的原始目标问题有很大的偏差，会损害BSGP的性能。

BSGP(Bipartite spectrum graph partitioning)共聚类，首先构建二部图$G=\{V, A\}$,V是点集，设$X\in{R}^{d \times n}$

$\boldsymbol{A}=\left[\begin{array}{cc} \boldsymbol{0} & \boldsymbol{X} \\ \boldsymbol{X}^{T} & \boldsymbol{0} \end{array}\right]$

feature cluster: $\boldsymbol{P}=\left[\boldsymbol{p}_{1 \cdot}^{T}, \cdots, \boldsymbol{p}_{d \cdot}^{T}\right]^{T} \in\{0,1\}^{d \times c}$

sample cluster: $\boldsymbol{Q}=\left[\boldsymbol{q}_{1 \cdot}^{T}, \cdots, \boldsymbol{q}_{d \cdot}^{T}\right]^{T} \in\{0,1\}^{n \times c}$

对聚类完成后的cluser定义（保证cluster中的元素比其他划分方法更好）：

feature cluster：

$\Omega_{l}=\{x_{i\cdot}:\sum_{j\in\Theta_{l}}X_{i j}\geq\sum_{i\in\Theta_{k}}X_{i j},\forall k=1,\cdot\cdot\cdot,c\}$

sample cluster：

$\Theta_{l}=\{x_j:\sum_{i\in\Omega,}X_{i j}\geq\sum_{i\in\Omega_{i}}X_{i j},\forall k=1,\cdot\cdot\cdot,c\}$

很容易看出$\Omega_l$与$\theta_l$之间存在递归关系，同时这也决定了BSGP基与diagonal co-cluster。

二划分的优化：

BGSP为了找到G最小的ncuts，优化如下的问题：

$\min _{\boldsymbol{y}} \frac{\boldsymbol{y}^{T} \boldsymbol{L} \boldsymbol{y}}{\boldsymbol{y}^{T} \boldsymbol{D} \boldsymbol{y}}, \text { s.t. } \boldsymbol{y} \in\{-1,1\}^{(d+n) \times 1}$

其中，$D$是度矩阵$D_{ii} = \textstyle\sum_{k}A_{i k}$

拉普拉斯矩阵： $L = D - A$

partition :

$y=[p^{T},q^{T}]^{T},p\in\{1,-1\}^{d\times1},q\in\{1,-1\}^{n\times1}$ 是indicator vector

由于上述优化目标是NP-complete problem,进行松弛：

$\operatorname*{min}_{q\neq0}{\frac{q^{T}L q}{q^{T}D q}},s.t.q^{T}D e=0$

其中$e$是$(d + n) \times 1$全1的向量,考虑到数据矩阵A的结构，可使用SVD计算$D_1^{-1/2}XD_2^{-1/2}$的第二小奇异值对应的向量来求解。$D1, D2$满足：

$\boldsymbol{D}=\left[\begin{array}{ll} \boldsymbol{D}_{1} & \\ & \boldsymbol{D}_{2} \end{array}\right]$

多个类群的扩展：

对于含有c个类群的情况，需要计算$l = log_2(c)$个left vectors U和right vectors V

构成一个L维度的数据集：

$\boldsymbol{Z}=\left[\begin{array}{l} \boldsymbol{D}_{1}^{-1 / 2} \boldsymbol{U} \\ \boldsymbol{D}_{2}^{-1 / 2} \boldsymbol{V} \end{array}\right]$

最后，需要用k-means算法对新的数据集Z进行聚类，其中Z的前d个结果对应X的特征聚类结果，后n个结果对应样本聚类结果。

BGSP中的问题：

需要一个后处理步骤来输出聚类结果
涉及奇异值分解(SVD)，其复杂度大于$O(n^2d)$。

Bilateral k-Means Algorithm for Fast Co-Clustering（IJCAI 2017）

优化目标

BGSP中多类群的优化目标为：

$\operatorname*{min}_{Y}\sum_{k=1}^{c}\frac{y_{k}^{T}L y_{k}}{y_{k}^{T}D y_{k}},s.t.{\cal Y}\in\Phi_{(d+n)\times c}$

由于$y_k^{T}Dy_k = Y^TDY$，因此优化目标转化为：

$\operatorname*{min}_{Y}Tr(Y^{I}LY\{Y^{I}D Y)^{-1}),s.t.Y\in\Phi_{(m+n)\chi c}$

由于$Y^{T}=[P^{T},Q^{T}]$，因此可以把A拆为X，即$T r(I-Y^{T}A Y(Y^{T}D Y)^{-1}) = T r(I-2P^{T}X Q(Y^{T}D Y)^{-1})$

优化目标转变为：

$\operatorname*{min}_{P.Q}T r(-P^{T}X Q(Y^{T}D Y)^{-1})$

$s.t.P\in\Phi_{d\times c},Q\in\Phi_{n\times c}$

为了得到二范数，添加$T r((Y^{T}D Y)^{-1}P^{T}P(Y^{T}D Y)^{-1}Q^{I}Q)$以及$T r(X^{T}X)$两项，得到优化目标：

$\operatorname*{min}_{P.Q}\|X-P(Y^{T}D Y)^{-1}Q^{T}\|_{F}^{2}$

$s.t.P\in\Phi_{d\times c},Q\in\Phi_{n\times c}$

$(Y^{T}D Y)^{-1}$是对角阵，求逆矩阵的开销很大，为了简化，用对角阵S代替，S也是待优化的参数：

$\operatorname*{min}_{P,O_{S}}\|X-P S Q^{T}\|_{F}^{2}$

$s.t.P\in\Phi_{d\times c},Q\in\Phi_{n\times c},\;S\in d i a g$

优化方法

使用两个命题来简化目标：

$J_{1}=||X-P S Q^{T}||_{F}^{2} =T r(X^{T}X)-2T r(Q^{T}X^{T}P S) +T r(S P^{T}P S Q^{T}Q)$

由于P和Q是indicator matrix，所以$P^{T}P$以及$Q^{T}Q$是对角阵，

由第一个命题：

$T r(Q^{T}X^{T}P S)=f({\cal S})^{T}f(P^{T}X Q)$

由第二个命题可知：

$T_{r}(S P^{T}P S Q^{T}Q)=T r(S P^{T}P Q^{T}Q S)=f(S)^{T}(P^{T}P Q^{T}Q)f(S)$

用$H$表示$P^T PQ^T Q$, $s$表示$f(s)$ $r$表示$f(P^T XQ)$,那么有：

$J_{1}=T r(X^{T}X)-2{\bf r}^{T}{\bf s}+{\bf s}^{T}{H}s$

求解s:

${\frac{\partial J_{1}}{\partial s}}=2(H s-r)=0$

$s=H^{-1}r$

由于H是对角阵，求逆很方便。

固定P、S,求Q：

$R = PS$

对每个sample进行如下优化：

$\operatorname*{min}_{Q}\|x_{\cdot i}-R q_{i\cdot}^{T}\|_{F}^{2}$

由于q是indicator，只会有一个1，那么就根据如下方式得出($r_k$是$R$的第k列)：

img
固定Q S，求P:

$L=SQ^T$

$\operatorname*{min}_{p}||x_{j}.-p^{T}_{j}L||_{F}^{2}$

$l_k$代表了L的第k行

2 Fasion recommendation

回顾《A Survey on Neural Recommendation: From Collaborative Filtering to Information-rich Recommendation》中，fashion recommendation是对Image information建模的代表任务，其目的在于增强可解释性。

DeepStyle: Learning User Preferences for Visual Recommendation（SIGIR 2017）

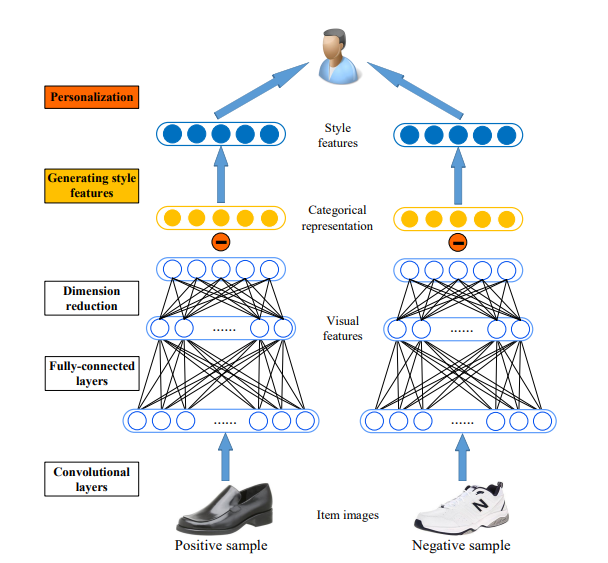
这篇文章将图片信息经过预训练好的cnn的到视觉embedding，聚类后发现相同类别的服装被聚类在一起（比如鞋子），而这与推荐任务不太符合，因为相似风格的商品往往会被同一个人同时购买（皮鞋配西装），但在视觉特征空间中却并不相似，这就为提升推荐效果带来了难度。因此作者提出一个商品（item）由风格（style）和类别（category）组成，即item = style + cate. 因此如上图，作者从商品的视觉特征向量中减除了该商品对应类别的隐含表达（类别的平均向量），进而得到了商品的风格特征向量.随后将向量输入到BPR框架中进行训练（对每个user采样正负商品样本对（正样本表示实际购买了的商品，负样本表示没有购买过的商品）），取得了很好的推荐效果。

Aesthetic-based Clothing Recommendation（www 2018）

传统的方法只考虑 CNN 抽取的图像特征；而本文考虑了图片中的美学特征对于推荐的影响；作者利用 BDN 从图片中学习美学特征，然后将其融合到 DCF 中，增强用户-产品，产品-时间矩阵，从而提高了推荐效果。

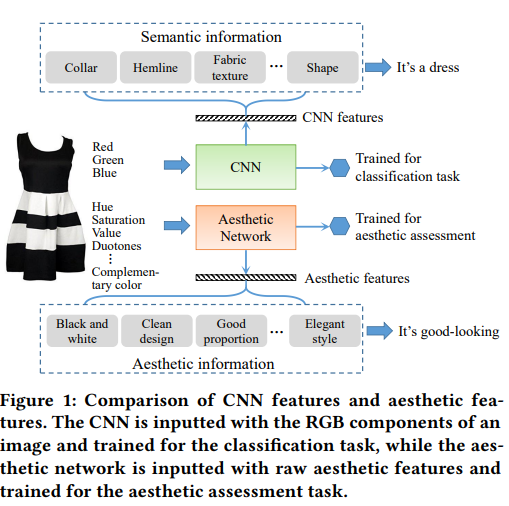
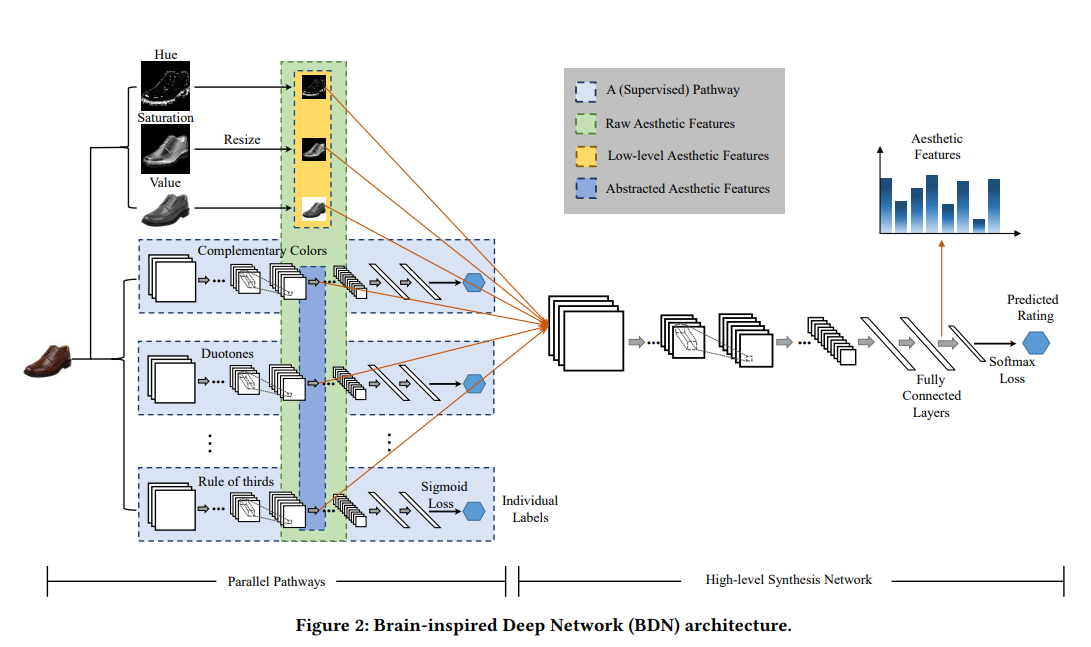
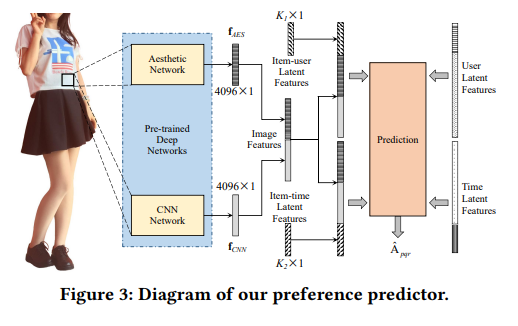
3 Boosting

回顾CART:

算法	支持模型	树结构	特征选择	连续值处理	缺失值处理	剪枝
ID3	分类	多叉树	信息增益	不支持	不支持	不支持
C4.5	分类	多叉树	信息增益比	支持	支持	支持
CART	分类回归	二叉树	基尼系数均方差	支持	支持	支持

C4.5决策树用较为复杂的熵（信息增益比）来度量，使用了相对较为复杂的多叉树，只能处理分类不能处理回归。CART(Classification And Regression Tree)做了改进，可以处理分类，也可以处理回归。

信息度量

ID3中使用了信息增益选择特征，增益大优先选择。C4.5中，采用信息增益比选择特征，减少因特征值多导致信息增益大的问题。CART分类树算法使用基尼系数来代替信息增益比，基尼系数代表了模型的不纯度，基尼系数越小，不纯度越低，特征越好。这和信息增益（比）相反。

　　假设K个类别，第k个类别的概率为$p_k$，概率分布的基尼系数表达式：

　　如果是二分类问题，第一个样本输出概率为p，概率分布的基尼系数表达式为：

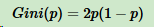
　　对于样本D，个数为$|D|$，假设K个类别，第k个类别的数量为$|C_k|$，则样本D的基尼系数表达式：

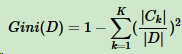
　　对于样本D，个数为$|D|$，根据特征A的某个值$a$，把D分成$|D1|$和$|D2|$，则在特征A的条件下，样本D的基尼系数表达式为：

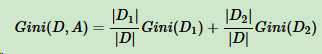
　　比较基尼系数和熵模型的表达式，二次运算比对数简单很多。尤其是二分类问题，更加简单。

对于二类分类，基尼系数和熵之半的曲线如下：

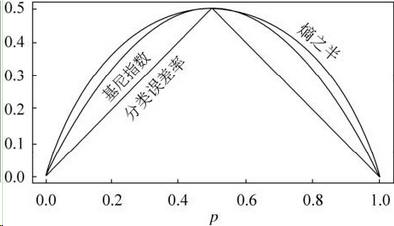
　　基尼系数和熵之半的曲线非常接近，因此，基尼系数可以做为熵模型的一个近似替代。

　　CART分类树算法每次仅对某个特征的值进行二分，而不是多分，这样CART分类树算法建立起来的是二叉树，而不是多叉树。

特征处理

对于连续的特征：

同C4.5一样将连续特征离散化，从小到大选相邻两样本值的平均数作为划分点，找基尼系数最小的划分。但与ID3、C4.5不同的是它后面还可以参与子节点的划分过程。

对于离散的特征：

ID3、C4.5，特征A被选取建立决策树节点，如果它有3个类别A1,A2,A3，我们会在决策树上建立一个三叉点，这样决策树是多叉树。CART采用的是不停的二分。会考虑把特征A分成{A1}和{A2,A3}、{A2}和{A1,A3}、{A3}和{A1,A2}三种情况，找到基尼系数最小的组合，比如{A2}和{A1,A3}，然后建立二叉树节点，一个节点是A2对应的样本，另一个节点是{A1,A3}对应的样本。由于这次没有把特征A的取值完全分开，后面还有机会对子节点继续选择特征A划分A1和A3。这和ID3、C4.5不同，在ID3或C4.5的一颗子树中，离散特征只会参与一次节点的建立。

流程

分类

输入:训练集D，基尼系数的阈值，样本个数阈值。

输出:决策树T。

递归建立CART分类树:

　　(1)、对于当前节点的数据集为D，如果样本个数小于阈值或没有特征，则返回决策子树，当前节点停止递归。

　　(2)、计算样本集D的基尼系数，如果基尼系数小于阈值，则返回决策树子树，当前节点停止递归。

　　(3)、计算当前节点现有的各个特征的各个特征值对数据集D的基尼系数，对于离散值和连续值的处理方法和基尼系数的计算见第二节。缺失值的处理方法和C4.5算法里描述的相同。

　　(4)、在计算出来的各个特征的各个特征值对数据集D的基尼系数中，选择基尼系数最小的特征A和对应的特征值a。根据这个最优特征和最优特征值，把数据集划分成两部分D1和D2，同时建立当前节点的左右节点，做节点的数据集D为D1，右节点的数据集D为D2。

　　(5)、对左右的子节点递归的调用1-4步，生成决策树。

　　对生成的决策树做预测的时候，假如测试集里的样本A落到了某个叶子节点，而节点里有多个训练样本。则对于A的类别预测采用的是这个叶子节点里概率最大的类别。
回归

与分类树不同：

不同。

　　(1)、分类树与回归树的区别在样本的输出，如果样本输出是离散值，这是分类树；样本输出是连续值，这是回归树。分类树的输出是样本的类别，回归树的输出是一个实数。

　　(2)、连续值的处理方法不同。

　　(3)、决策树建立后做预测的方式不同。

　　分类模型：采用基尼系数的大小度量特征各个划分点的优劣。

　　回归模型：采用和方差度量，度量目标是对于划分特征A，对应划分点s两边的数据集D1和D2，求出使D1和D2各自集合的均方差最小，同时D1和D2的均方差之和最小。

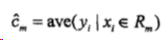
img

表达式为：

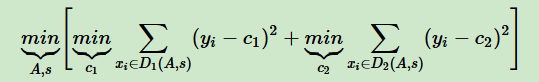
img

其中，c1为D1的样本输出均值，c2为D2的样本输出均值。

　　对于决策树建立后做预测的方式，CART分类树采用叶子节点里概率最大的类别作为当前节点的预测类别。回归树输出不是类别，采用叶子节点的均值或者中位数来预测输出结果。

boosting

bagging和boosting是集成学习的两种代表性范式，bagging的个体弱学习器的训练集是通过随机采样得到的，学习器之间没有强依赖关系。boosting相反，每次训练都期望纠正之前的错误，学习器之间存在强依赖关系。Boosting主要关注降低偏差，因此Boosting能基于泛化性能相当弱的学习器构建出很强的集成；Bagging主要关注降低方差，因此它在不剪枝的决策树、神经网络等学习器上效用更为明显。

工作机制

boosting方法的工作机制是首先从训练集用初始权重训练出一个弱学习器1，根据弱学习的学习误差率表现来更新训练样本的权重，使得之前弱学习器1学习误差率高的训练样本点的权重变高，使得这些误差率高的点在后面的弱学习器2中得到更多的重视。然后基于调整权重后的训练集来训练弱学习器2.，如此重复进行，直到弱学习器数达到事先指定的数目T，最终将这T个弱学习器通过集合策略进行整合，得到最终的强学习器。　　

boosting家族算法一般需要解决：

1）如何计算学习误差率e?

2)如何得到弱学习器权重系数$α$?

　3)如何更新样本权重D?

4)使用何种结合策略？

Adaboost

基本思路

训练样本：

$T=\{(x_,y_1),(x_2,y_2), ...(x_m,y_m)\}$

训练集的在第k个弱学习器的输出权重为(第一个权重1/m，后面逐渐调整)

$D(k) = (w_{k1}, w_{k2}, ...w_{km}) ;\;\; w_{1i}=\frac{1}{m};\;\; i =1,2...m$

分类问题

多元分类是二元分类的推广，这里首先考虑二分类，输出为{-1,1}

1）第k个弱分类器$G_k(x)$在训练集上的加权误差率为

$e_k = P(G_k(x_i) \neq y_i) = \sum\limits_{i=1}^{m}w_{ki}I(G_k(x_i) \neq y_i)$

2）第k个弱分类器$G_k(x)$权重系数为：

$\alpha_k = \frac{1}{2}log\frac{1-e_k}{e_k}$

从上式可以看出，如果分类误差率$ek$越大，则对应的弱分类器权重系数$αk$越小。也就是说，误差率小的弱分类器权重系数越大。

3)样本权重D:假设第k个弱分类器的样本集权重系数为$D(k) = (w_{k1}, w_{k2}, ...w_{km})$，则对应的第k+1个弱分类器的样本集权重系数为:

$w_{k+1,i} = \frac{w_{ki}}{Z_K}exp(-\alpha_ky_iG_k(x_i))$

其中规范化因子$Z_k = \sum\limits_{i=1}^{m}w_{ki}exp(-\alpha_ky_iG_k(x_i))$

计算公式可以看出，如果第i个样本分类错误，则$y_iG_k(x_i) < 0$，导致样本的权重在第k+1个弱分类器中增大，如果分类正确，则权重在第k+1个弱分类器中减少.

4)集成策略：加权表决法

$f(x) = sign(\sum\limits_{k=1}^{K}\alpha_kG_k(x))$

对于Adaboost多元分类算法，其实原理和二元分类类似，最主要区别在弱分类器的系数上。比如Adaboost SAMME算法，它的弱分类器的系数：

$\alpha_k = \frac{1}{2}log\frac{1-e_k}{e_k} + log(R-1)$

其中R为类别数
回归问题（Adaboost R2）

数据权重: $D(1) = (w_{11}, w_{12}, ...w_{1m}) ;\;\; w_{1i}=\frac{1}{m};\;\; i =1,2...m$

1）对于弱学习器：计算最大误差$E_k= max|y_i - G_k(x_i)|\;i=1,2...m$

2）计算每个样本的相对误差:

线性：$e_{ki}= \frac{|y_i - G_k(x_i)|}{E_k}$

平方：$e_{ki}= \frac{(y_i - G_k(x_i))^2}{E_k^2}$

指数：$e_{ki}= 1 - exp（\frac{-|y_i -G_k(x_i)|}{E_k}）$

3）回归误差率为：$e_k = \sum\limits_{i=1}^{m}w_{ki}e_{ki}$

4）弱学习器的系数：$\alpha_k =\frac{e_k}{1-e_k}$

5）新的数据权重：$w_{k+1,i} = \frac{w_{ki}}{Z_k}\alpha_k^{1-e_{ki}}$,$Z_k = \sum\limits_{i=1}^{m}w_{ki}\alpha_k^{1-e_{ki}}$

6）最终的集成学习器：$f(x) =G_{k^*}(x)$, $G_{k^*}(x)=G_k(x)ln\frac{1}{\alpha_k} , k=1,2,....K$

损失函数以及各权重推导

从分类器角度，adaboost是多个分类器叠加：

第k-1轮的强学习器为：$f_{k-1}(x) = \sum\limits_{i=1}^{k-1}\alpha_iG_{i}(x)$

第k轮：$f_{k}(x) = \sum\limits_{i=1}^{k}\alpha_iG_{i}(x)$

因此可以得到迭代关系：$f_{k}(x) = f_{k-1}(x) + \alpha_kG_k(x)$

adaboost的损失函数为指数函数：

$\underbrace{arg\;min\;}_{\alpha, G} \sum\limits_{i=1}^{m}exp(-y_if_{k}(x))$

将迭代关系代入：$L(\alpha_k, G_k(x)) = \underbrace{arg\;min\;}_{\alpha, G}\sum\limits_{i=1}^{m}exp[(-y_i) (f_{k-1}(x) + \alpha G(x))]$

令$w_{ki}^{’} = exp(-y_if_{k-1}(x))$, 可知该值与$\alpha 、G$无关，仅与$f_{k-1}$有关：$L(\alpha_k, G_k(x)) = \underbrace{arg\;min\;}_{\alpha, G}\sum\limits_{i=1}^{m}w_{ki}^{’}exp[-y_i\alpha G(x)]$

求$G_k(x)$：

$\begin{align} \sum\limits_{i=1}^mw_{ki}^{'}exp(-y_i\alpha G(x_i)) &= \sum\limits_{y_i =G_k(x_i)}w_{ki}^{'}e^{-\alpha} + \sum\limits_{y_i \ne G_k(x_i)}w_{ki}^{'}e^{\alpha} \\& = (e^{\alpha} - e^{-\alpha})\sum\limits_{i=1}^mw_{ki}^{'}I(y_i \ne G_k(x_i)) + e^{-\alpha}\sum\limits_{i=1}^mw_{ki}^{'} \end{align}$

得：$G_k(x) = \underbrace{arg\;min\;}_{G}\sum\limits_{i=1}^{m}w_{ki}^{’}I(y_i \neq G(x_i))$
求$\alpha$：G代入损失函数$L$，并对$$求导，令其为零：$_k = log$

$e_k = \frac{\sum\limits_{i=1}^{m}w_{ki}^{’}I(y_i \neq G(x_i))}{\sum\limits_{i=1}^{m}w_{ki}^{’}} = \sum\limits_{i=1}^{m}w_{ki}I(y_i \neq G(x_i))$
利用迭代关系以及$w_{ki}^{’} = exp(-y_if_{k-1}(x))$得到w迭代公式：

$w_{k+1,i}^{’} = w_{ki}^{’}exp[-y_i\alpha_kG_k(x)]$

正则化项

对学习器迭代添加正则项：$f_{k}(x) = f_{k-1}(x) + \nu\alpha_kG_k(x)$，$\nu$的取值范围为$\nu \in [0,1]$。对于同样的训练集学习效果，较小的$$意味着我们需要更多的弱学习器的迭代次数。

总结

最广泛的Adaboost弱学习器是决策树和神经网络。对于决策树，Adaboost分类用了CART分类树，而Adaboost回归用了CART回归树。

　　　　Adaboost的主要优点有：

　　　　1）Adaboost作为分类器时，分类精度很高

　　　　2）在Adaboost的框架下，可以使用各种回归分类模型来构建弱学习器，非常灵活。

　　　　3）作为简单的二元分类器时，构造简单，结果可理解。

　　　　4）不容易发生过拟合

　　　　Adaboost的主要缺点有：

　　　　1）对异常样本敏感，异常样本在迭代中可能会获得较高的权重，影响最终的强学习器的预测准确性。

GBDT

https://zhuanlan.zhihu.com/p/89572181

GBDT(Gradient Boosting Decision Tree) 又叫 MART（Multiple Additive Regression Tree)，是一种迭代的决策树算法，GBDT中的树是回归树（不是分类树），GBDT用来做回归预测，调整后也可以用于分类。

回顾：

回归树（用最小均方误差来进行划分）：
提升树：迭代多颗树共同决策，每一棵树是之前的所有树的结论和残差。

需要解决： 1）如何计算学习误差率e?（残差）

2)如何得到弱学习器权重系数$α$?（这一棵树的权重）

　3)如何更新样本权重D?（下一棵树的学习）

4)使用何种结合策略？（决策）

GDBT关注了如何学习残差的问题，当损失函数时平方损失和指数损失函数时，每一步的优化很简单（如adaboost），但是对于更一般的损失函数，每一步的优化就不容易了。

针对这一问题，Freidman提出了梯度提升算法：利用最速下降的近似方法，即利用损失函数的负梯度在当前模型的值，作为回归问题中提升树算法的残差的近似值，拟合一个回归树：

初始化：f0仅仅是只有一个根节点的树，$\gamma$是划分值，让loss最小
循环部分：
1. 对每一个样本计算负梯度（样本权重）
2. 利用（x, r）拟合cart回归树，对应的叶子节点区域是$R_{jm}$，j是叶子结点个数
c.对叶子节点计算最佳的拟合值（学习残差）

d.更新强学习器$f_{m}(x)=f_{m-1}(x)+\sum_{j=1}^{J_{m}} \gamma_{j m} I\left(x \in R_{j m}\right)$
汇总：$f(x)=f_{0}(x)+\sum_{m=1}^{M}\sum_{j=1}^{J_{m}} \gamma_{j m} I\left(x \in R_{j m}\right)$

调参时的问题：

树的深度很少就能达到很高的精度（6，对于普通决策树和随机森林需要15+）。泛化误差可以分解为两部分，偏差（bias)和方差(variance)。boosting关注偏差，bagging关注方差。因此对boosting而言，弱学习器的拟合能力不能太强（方差小），不然会导致过拟合。而bagging采样不同的数据来进行弱分类器的训练，因此不容易过拟合。

XGBoost——GDBT的更快实现1（待补充）

https://www.cnblogs.com/mantch/p/11164221.html

https://zhuanlan.zhihu.com/p/86816771

LightGBM——GDBT的更快实现2（待补充）

https://zhuanlan.zhihu.com/p/99069186